
(1)求證:AM∥平面BDE;
(2)求二面角A-DF-B的大小;
(3)試在線段AC上確定一點P,使得PF與BC所成的角是60°.

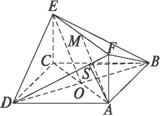
(1)證明:記AC與BD的交點為O,連結(jié)OE,
∵O,M分別是AC,EF的中點,ACEF是矩形,
∴四邊形AOEM是平行四邊形.
∴AM∥OE.
∵OE![]() 平面BDE,AM
平面BDE,AM![]() 平面BDE,
平面BDE,
∴AM∥平面BDE.
(2)解:在平面AFD中,過A點作AS⊥DF于點S,連結(jié)BS,
∵AB⊥AF,AB⊥AD,AD∩AF=A,
∴AB⊥平面ADF.
∴AS是BS在平面ADF上的射影.
由三垂線定理得BS⊥DF,
∴∠BSA是二面角ADFB的平面角.
在Rt△ASB中,AS=![]() ,AB=
,AB=![]() ,
,
∴tan∠ASB=![]() ,∠ASB=60°.
,∠ASB=60°.
∴二面角ADFB的大小為60°.
(3)解:設(shè)CP=t(0≤t≤2),作PQ⊥AB于Q,則PQ∥BC,
∵PQ⊥AB,PQ⊥AF,AB∩AF=A,
∴PQ⊥平面ABF,QF![]() 平面ABF.
平面ABF.
∴PQ⊥QF.
在Rt△PQF中,∠FPQ=60°,PF=2PQ,
∵△PAQ為等腰直角三角形,
∴PQ=![]() (2-t).
(2-t).
又∵△PAF為直角三角形,
∴PF=![]() .
.
∴![]() =2×
=2×![]() (2-t).
(2-t).
∴t=1或t=3(舍去),
即點P是AC的中點.


科目:高中數(shù)學(xué) 來源: 題型:
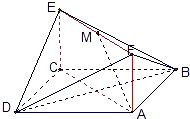 如圖,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如圖,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,已知正方形ABCD的邊長為1,過正方形中心O的直線MN分別交正方形的邊AB,CD于M,N,則當(dāng)
如圖,已知正方形ABCD的邊長為1,過正方形中心O的直線MN分別交正方形的邊AB,CD于M,N,則當(dāng)| MN |
| BN |
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=
如圖,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=| 2 |
| 2 |
| ME |
| FM |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如圖,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 (2012•深圳二模)如圖,已知正方形ABCD在水平面上的正投影(投影線垂直于投影面)是四邊形A′B′C′D′,其中A與A'重合,且BB′<DD′<CC′.
(2012•深圳二模)如圖,已知正方形ABCD在水平面上的正投影(投影線垂直于投影面)是四邊形A′B′C′D′,其中A與A'重合,且BB′<DD′<CC′.| 2 |
| 5 |
| 6 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com