
(本題滿分15分)
已知函數(shù)f (x )=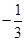 ax
3 + x2 + 2 ( a ≠ 0 ) .
ax
3 + x2 + 2 ( a ≠ 0 ) .
(Ⅰ) 試討論函數(shù)f (x )的單調(diào)性;
(Ⅱ) 若a>0,求函數(shù)f (x ) 在[1,2]上的最大值.
解: (1) ①當(dāng)a>0時(shí), f(x)在(-∞,0),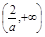 上是減函數(shù),在
上是減函數(shù),在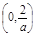 上是增函數(shù).
上是增函數(shù).
②當(dāng)a<0時(shí), f(x)在(-∞, 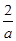 ),(0, +∞)上是增函數(shù),在(
),(0, +∞)上是增函數(shù),在(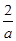 ,0)上是減函數(shù).
,0)上是減函數(shù).
(2)當(dāng)0<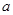 <1時(shí),f(x)的最大值為3-
<1時(shí),f(x)的最大值為3-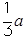 ,
,
當(dāng)1≤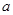 ≤2時(shí),f(x)的最大值為
≤2時(shí),f(x)的最大值為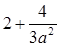 ,
,
當(dāng)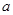 >2時(shí),f(x)的最大值為
>2時(shí),f(x)的最大值為 .
.
【解析】本試題主要是考查了函數(shù)單調(diào)性和函數(shù)最值的求解的綜合運(yùn)用。
(1)根據(jù)已知條件,對(duì)于參數(shù)a進(jìn)行分類討論,判定單調(diào)性得到結(jié)論。
(2)在第一問(wèn)的基礎(chǔ)上,進(jìn)一步對(duì)于不同情況下的單調(diào)性分別研究得到最值。
選做題:(參加IB學(xué)習(xí)的學(xué)生必須做,不參加IB學(xué)習(xí)的學(xué)生原則上不要做)
題目:(本題滿分值為10分)
解: (1)
∵f(x)=- ax3+x2+2
(a≠0),∴
ax3+x2+2
(a≠0),∴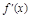 = -ax2+2x.
= -ax2+2x.
①當(dāng)a>0時(shí),令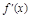 >0,即-ax2+2x>0,得0<x<
>0,即-ax2+2x>0,得0<x<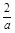 .
.
∴f(x)在(-∞,0),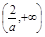 上是減函數(shù),在
上是減函數(shù),在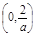 上是增函數(shù). ………………4分
上是增函數(shù). ………………4分
②當(dāng)a<0時(shí),令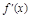 >0,即-ax2+2x>0,得x>0,或x<
>0,即-ax2+2x>0,得x>0,或x<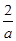 .
.
∴f(x)在(-∞, 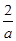 ),(0, +∞)上是增函數(shù),在(
),(0, +∞)上是增函數(shù),在(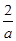 ,0)上是減函數(shù).………………8分
,0)上是減函數(shù).………………8分
(2)由(1)得:
①當(dāng)0<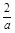 <1,即a>2時(shí),f(x)在(1,2)上是減函數(shù),
<1,即a>2時(shí),f(x)在(1,2)上是減函數(shù),
∴f(x)max=f(1)=3-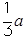 . ……………10分
. ……………10分
②當(dāng)1≤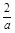 ≤2,即1≤a≤2時(shí),f(x)在
≤2,即1≤a≤2時(shí),f(x)在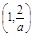 上是增函數(shù),在
上是增函數(shù),在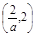 上是減函數(shù),
上是減函數(shù),
∴f(x)max=f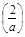 =
=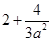 .
………12分
.
………12分
③當(dāng)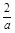 >2時(shí),即0<
>2時(shí),即0<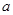 <1時(shí),f(x)在(1,2)上是增函數(shù),
<1時(shí),f(x)在(1,2)上是增函數(shù),
∴f(x)max=f(2)=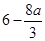 .
……………14分
.
……………14分
綜上所述,當(dāng)0<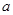 <1時(shí),f(x)的最大值為3-
<1時(shí),f(x)的最大值為3-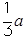 ,
,
當(dāng)1≤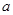 ≤2時(shí),f(x)的最大值為
≤2時(shí),f(x)的最大值為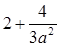 ,
,
當(dāng)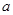 >2時(shí),f(x)的最大值為
>2時(shí),f(x)的最大值為 . ………………15分
. ………………15分



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:2010-2011年江蘇省如皋市五校高二下學(xué)期期中考試?yán)砜茢?shù)學(xué) 題型:解答題
((本題滿分15分)
某有獎(jiǎng)銷售將商品的售價(jià)提高120元后允許顧客有3次抽獎(jiǎng)的機(jī)會(huì),每次抽獎(jiǎng)的方法是在已經(jīng)設(shè)置并打開了程序的電腦上按“Enter”鍵,電腦將隨機(jī)產(chǎn)生一個(gè) 1~6的整數(shù)數(shù)作為號(hào)碼,若該號(hào)碼是3的倍數(shù)則顧客獲獎(jiǎng),每次中獎(jiǎng)的獎(jiǎng)金為100元,運(yùn)用所學(xué)的知識(shí)說(shuō)明這樣的活動(dòng)對(duì)商家是否有利。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年浙江省招生適應(yīng)性考試文科數(shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分15分)設(shè)函數(shù) .
.
(Ⅰ)若函數(shù) 在
在 上單調(diào)遞增,在
上單調(diào)遞增,在 上單調(diào)遞減,求實(shí)數(shù)
上單調(diào)遞減,求實(shí)數(shù) 的最大值;
的最大值;
(Ⅱ)若 對(duì)任意的
對(duì)任意的 ,
, 都成立,求實(shí)數(shù)
都成立,求實(shí)數(shù) 的取值范圍.
的取值范圍.
注: 為自然對(duì)數(shù)的底數(shù).
為自然對(duì)數(shù)的底數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年浙江省溫州市十校聯(lián)合體高三上學(xué)期期初摸底文科數(shù)學(xué) 題型:解答題
(本題滿分15分)已知直線 與曲線
與曲線 相切
相切
1)求b的值;
2)若方程 在
在 上恰有兩個(gè)不等的實(shí)數(shù)根
上恰有兩個(gè)不等的實(shí)數(shù)根 ,求
,求
①m的取值范圍;
②比較 的大小
的大小
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年浙江省溫州市十校聯(lián)合體高三上學(xué)期期中考試文科數(shù)學(xué) 題型:解答題
(本題滿分15分)已知拋物線 :
: (
( ),焦點(diǎn)為
),焦點(diǎn)為 ,直線
,直線 交拋物線
交拋物線 于
于 、
、 兩點(diǎn),
兩點(diǎn), 是線段
是線段 的中點(diǎn),
的中點(diǎn),
過(guò) 作
作 軸的垂線交拋物線
軸的垂線交拋物線 于點(diǎn)
于點(diǎn) ,
,
(1)若拋物線 上有一點(diǎn)
上有一點(diǎn) 到焦點(diǎn)
到焦點(diǎn) 的距離為
的距離為 ,求此時(shí)
,求此時(shí) 的值;
的值;
(2)是否存在實(shí)數(shù) ,使
,使 是以
是以 為直角頂點(diǎn)的直角三角形?若存在,求出
為直角頂點(diǎn)的直角三角形?若存在,求出 的值;若不存在,說(shuō)明理由。
的值;若不存在,說(shuō)明理由。

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年浙江省六校高三第一次聯(lián)考文科數(shù)學(xué) 題型:解答題
(本題滿分15分)
已知函數(shù)
(1)求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)設(shè) ,若
,若 在
在 上不單調(diào)且僅在
上不單調(diào)且僅在 處取得最大值,求
處取得最大值,求 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com