
已知點集L={(x,y)|y=m·n},其中m=(2x-2b,1),n=(1,1+2b),點列Pn(an,bn)在點集L中,P1為L的軌跡與y軸的交點,已知數列{an}為等差數列,且公差為1,n∈N*.
(1)求數列{an},{bn}的通項公式;
(2)求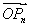 ·OPn+1的最小值;
·OPn+1的最小值;
(3)設cn=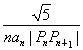 (n≥2),求c2+c3+c4+…+cn的值.
(n≥2),求c2+c3+c4+…+cn的值.
(1)bn=2n-1(n∈N*).(2)3.(3)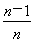
【解析】(1)由y=m·n,
m=(2x-2b,1), n=(1,1+2b),得y=2x+1,
即L的軌跡方程為y=2x+1.
∵P1為L的軌跡與y軸的交點,
∴P1(0,1),則a1=0,b1=1,
∵數列{an}為等差數列,且公差為1,
∴an=n-1(n∈N*),
代入y=2x+1,得bn=2n-1(n∈N*).
(2)∵Pn(n-1,2n-1),∴Pn+1(n,2n+1),
∴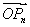 ·OPn+1=(n-1,2n-1)·(n,2n+1)
·OPn+1=(n-1,2n-1)·(n,2n+1)
=5n2-n-1=5 2-
2-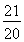 .
.
∵n∈N*,
∴當n=1時,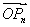 ·OPn+1有最小值,為3.
·OPn+1有最小值,為3.
(3)當n≥2時,由Pn(n-1,2n-1),
得an·|PnPn+1|=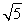 (n-1),
(n-1),
cn=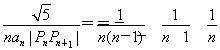 ,
,
∴c2+c3+…+cn=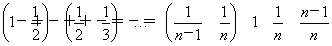


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)仿真模擬卷1練習卷(解析版) 題型:選擇題
已知函數f(x)= 若函數y=f(x)-2有3個零點,則實數a的值為( )
若函數y=f(x)-2有3個零點,則實數a的值為( )
A.-4 B.-2 C.0 D.2
查看答案和解析>>
科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)專題階段評估模擬卷5練習卷(解析版) 題型:選擇題
過雙曲線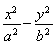 =1(a>0,b>0)的左焦點F(-c,0)(c>0)作圓x2+y2=
=1(a>0,b>0)的左焦點F(-c,0)(c>0)作圓x2+y2=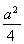 的切線,交雙曲線右支于點P,切點為E,若
的切線,交雙曲線右支于點P,切點為E,若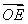 =
=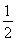 (
(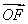 +
+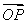 ),則雙曲線的離心率為( )
),則雙曲線的離心率為( )
A. 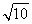 B.
B. 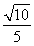 C.
C. 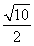 D.
D.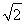
查看答案和解析>>
科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)專題階段評估模擬卷4練習卷(解析版) 題型:填空題
如圖所示,在邊長為4的正方形紙片ABCD中,AC與BD相交于點O,剪去△AOB,將剩余部分沿OC,OD折疊,使OA,OB重合,則以A,B,C,D,O為頂點的四面體的體積為________.
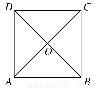
查看答案和解析>>
科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)專題階段評估模擬卷4練習卷(解析版) 題型:選擇題
設m,n是兩條不同的直線,α,β,γ是三個不同的平面,有以下四個命題:
①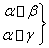 ⇒β∥γ②
⇒β∥γ②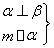 ⇒m⊥β③
⇒m⊥β③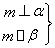 ⇒α⊥β④
⇒α⊥β④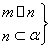 ⇒m∥α
⇒m∥α
其中正確的命題是( )
A.①④ B.②③ C.①③ D.②④
查看答案和解析>>
科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)專題階段評估模擬卷3練習卷(解析版) 題型:解答題
已知等差數列{an}的前n項和Sn滿足S3=0,S5=-5.
(1)求{an}的通項公式;
(2)求數列 的前n項和.
的前n項和.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)專題階段評估模擬卷3練習卷(解析版) 題型:選擇題
已知數列{an},{bn}滿足a1=b1=3,an+1-an=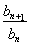 =3,n∈N*,若數列{cn}滿足cn=ban,則c2 013=( )
=3,n∈N*,若數列{cn}滿足cn=ban,則c2 013=( )
A.92 012 B.272 012 C.92 013 D.272 013
查看答案和解析>>
科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)專題階段評估模擬卷2練習卷(解析版) 題型:填空題
若函數f(x)=2sin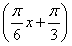 (-2<x<10)的圖象與x軸交于點A,過點A的直線l與函數的圖象交于B、C兩點,則(
(-2<x<10)的圖象與x軸交于點A,過點A的直線l與函數的圖象交于B、C兩點,則(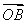 +
+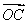 )·
)· =________.
=________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練解答題押題練C組練習卷(解析版) 題型:解答題
已知函數f(x)=x2-(1+2a)x+aln x(a為常數).
(1)當a=-1時,求曲線y=f(x)在x=1處切線的方程;
(2)當a>0時,討論函數y=f(x)在區間(0,1)上的單調性,并寫出相應的單調區間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com