求過拋物線y=ax2+bx+c(a≠0)上一點P(x,y)處的切線方程,并由此證實拋物線的光學性質.
【答案】
分析:為求斜率,先求導函數,得到切線方程,根據拋物線焦點:F(
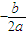
,
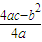
),它關于切線的對稱點之橫坐標為x
,
說明從焦點發出的光線射到(x
,y
)經拋物面反射后反射光線平行于對稱軸,反之亦然,與對稱軸平行的光線被拋物面反射后必聚匯于焦點.
解答:解:顯然,y
=ax
2+bx
+c
y′=2ax+b故在P點處切線斜率為2ax
+b,
切線方程y-(ax
2+bx
+c)=(2ax
+b)(x-x
),
亦即y=(2ax
+b)x-ax
2+c.
由于y=ax
2+bx+c按向量=
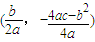
平移即得到y=ax
2,
只須證明過其上一點(x
,ax
2)的切線l:y=2ax
x-ax
2
滿足:焦點關于l的對稱點為(m,n).
當x
≠0時
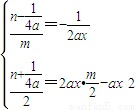
,消去n.知m=x
.
當x
=0時,切線為y=0,F之對稱點橫坐標顯然是0,
故從焦點發出的光線射到(x
,ax
2)后被拋物面反射后的方程為x=x
(與對稱軸平行);
反之,與對稱軸平行的光線被拋物面反射后必聚匯于焦點
點評:本題主要考查了利用導數研究曲線上某點切線方程,要求過曲線上一點處的切線方程,一般先求出該點的導數值(斜率),再用點斜式寫出后化簡,同時我們還可以據此寫出該點處的法線方程,考查轉化思想,屬于基礎題.

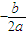 ,
,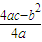 ),它關于切線的對稱點之橫坐標為x,
),它關于切線的對稱點之橫坐標為x,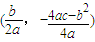 平移即得到y=ax2,
平移即得到y=ax2,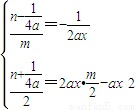 ,消去n.知m=x.
,消去n.知m=x.

 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案