
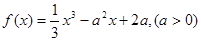
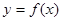 的單調區間;
的單調區間;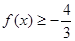 ,求
,求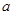 的取值范圍.
的取值范圍. 目標測試系列答案
目標測試系列答案科目:高中數學 來源:不詳 題型:解答題
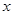 個月內,對某種商品的需求總量
個月內,對某種商品的需求總量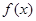 (萬件)近似滿足:
(萬件)近似滿足: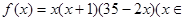 N*,且
N*,且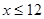 )
)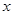 個月的需求量
個月的需求量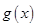 (萬件)與月份
(萬件)與月份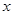 的函數關系式,并求出哪個月份的需求量超過
的函數關系式,并求出哪個月份的需求量超過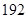 萬件;
萬件;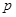 萬件(不包含積壓商品),要保證每月都滿足供應,
萬件(不包含積壓商品),要保證每月都滿足供應,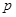 應至少為多少萬件?(積壓商品轉入下月繼續銷售)
應至少為多少萬件?(積壓商品轉入下月繼續銷售)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com