
(本小題9分)某家公司每月生產兩種布料A和B,所有原料是三種不同顏色的羊毛,下表給出了生產每匹每種布料所需的羊毛量,以及可供使用的每種顏色的羊毛的總量。
|
羊毛顏色 |
每匹需要 / kg |
供應量/ kg |
|
|
布料A |
布料B |
||
|
紅 |
4 |
4 |
1400 |
|
綠 |
6 |
3 |
1800 |
|
黃 |
2 |
6 |
1800 |
已知生產每匹布料A、B的利潤分別為120元、80元。那么如何安排生產才能夠產生最大的利潤?最大的利潤是多少?
該公司每月生產布料A、B分別為250 、100匹時,產生最大的利潤,最大的利潤是38000 元。
【解析】本試題主要是考查了線性規劃的運用,求解最優解問題的實際運用。
首先設每月生產布料A、B分別為x匹、y匹,利潤為Z元,那么
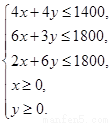 ①
①
目標函數為 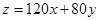
根據題意利用線性約束條件作出可行域,然后借助于圖像,平移目標函數,得到目標函數的最優解。
設每月生產布料A、B分別為x匹、y匹,利潤為Z元,那么
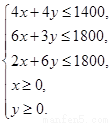 ①
①
目標函數為
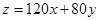
作出二元一次不等式①所表示的
平面區域(陰影部分)即可行域。
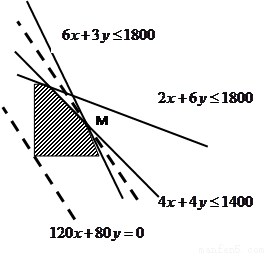
把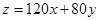 變形為
變形為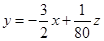 ,得到斜率為
,得到斜率為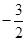 ,在軸上的截距為
,在軸上的截距為 ,隨z變化的一族平行直線。如圖可以看出,當直線
,隨z變化的一族平行直線。如圖可以看出,當直線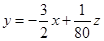 經過可行域上
經過可行域上
M時,截距 最大,即z最大。 解方程組
最大,即z最大。 解方程組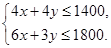 得M的坐標為x=250 , y=100 所以
得M的坐標為x=250 , y=100 所以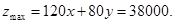
答:該公司每月生產布料A、B分別為250 、100匹時,產生最大的利潤,最大的利潤是38000 元。


 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:高中數學 來源:2012屆福建省福州八中高二上學期期中考試理科數學 題型:解答題
.(本小題9分)某家公司每月生產兩種布料A和B,所有原料是三種不同顏色的羊毛,下表給出了生產每匹每種布料所需的羊毛量,以及可供使用的每種顏色的羊毛的總量
| 羊毛顏色 | 每匹需要 / kg | 供應量/ kg | |
| 布料A | 布料B | ||
| 紅 | 4 | 4 | 1400 |
| 綠 | 6 | 3 | 1800 |
| 黃 | 2 | 6 | 1800 |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省高二上學期期中考試理科數學 題型:解答題
.(本小題9分)某家公司每月生產兩種布料A和B,所有原料是三種不同顏色的羊毛,下表給出了生產每匹每種布料所需的羊毛量,以及可供使用的每種顏色的羊毛的總量
|
羊毛顏色 |
每匹需要 / kg |
供應量/ kg |
|
|
布料A |
布料B |
||
|
紅 |
4 |
4 |
1400 |
|
綠 |
6 |
3 |
1800 |
|
黃 |
2 |
6 |
1800 |
已知生產每匹布料A、B的利潤分別為120元、80元。那么如何安排生產才能夠產生最大的利潤?最大的利潤是多少?
查看答案和解析>>
科目:高中數學 來源:2010-2011年福建省四地六校高二下學期第一次月考數學理卷 題型:解答題
((本小題12分)某造船公司年造船量是20艘,已知造船 艘的產值函數為
艘的產值函數為
 (單位:萬元),成本函數為
(單位:萬元),成本函數為 (單位:萬元),又在經濟學中,函數
(單位:萬元),又在經濟學中,函數 的邊際函數
的邊際函數 定義為
定義為 。
。
(Ⅰ)求利潤函數 及邊際利潤函數
及邊際利潤函數 ;(提示:利潤=產值-成本)
;(提示:利潤=產值-成本)
(Ⅱ)問年造船量安排多少艘時,可使公司造船的年利潤最大?
(Ⅲ)求邊際利潤函數 單調遞減時
單調遞減時 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源:2010-2011年新疆農七七師高級中學高二下學期第一學段考試理科數學 題型:解答題
(本小題12分)
某造船公司年造船量是20艘,已知造船 艘的產值函數為
艘的產值函數為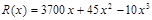 (單位:萬元),成本函數為
(單位:萬元),成本函數為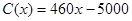 (單位:萬元),又在經濟學中,函數
(單位:萬元),又在經濟學中,函數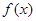 的邊際函數
的邊際函數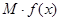 定義為
定義為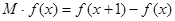 。
。
(Ⅰ)求利潤函數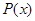 及邊際利潤函數
及邊際利潤函數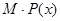 ;(提示:利潤=產值-成本)
;(提示:利潤=產值-成本)
(Ⅱ)問年造船量安排多少艘時,可使公司造船的年利潤最大?
(Ⅲ)求邊際利潤函數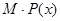 單調遞減時
單調遞減時 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com