
如圖,四邊形ABCD為矩形,AD  平面ABE,AE=EB=BC=2,F為CE上的點.且BF
平面ABE,AE=EB=BC=2,F為CE上的點.且BF  平面ACE.
平面ACE.

(1)求證:平面ADE 平面BCE;
平面BCE;
(2)求四棱錐E-ABCD的體積;
(3)設M在線段AB上,且滿足AM=2MB,試在線段CE上確定一點N,使得MN 平面DAE.
平面DAE.
(1)略; (2) 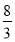 ;(3)N為線段CE上靠近C點的一個三等分點.
;(3)N為線段CE上靠近C點的一個三等分點.
【解析】
試題分析:(1)由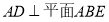 且
且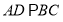 可得
可得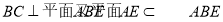 ,所以有
,所以有
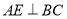 ,同理可得
,同理可得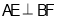 ,
,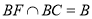
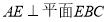 ,所以
,所以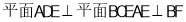 .
.
(2)四棱錐的體積 ,
,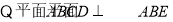
 四棱錐的高即點E到AB的距離,所以
四棱錐的高即點E到AB的距離,所以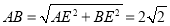 ,四棱錐E-ABCD的體積為
,四棱錐E-ABCD的體積為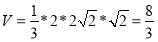 .
.
(3)在三角形ABC過M點作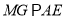 交
交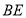 于
于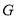 點,在三角形BEC中過G點作
點,在三角形BEC中過G點作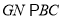 交EC與N點,連MN,則由比例關系易得
交EC與N點,連MN,則由比例關系易得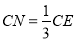 ,
,
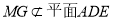
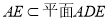
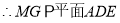 同理,
同理,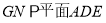
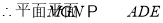 又
又
 N為線段CE上靠近C點的一個三等分點.
N為線段CE上靠近C點的一個三等分點.
試題解析:(1) 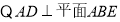 且
且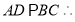
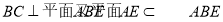

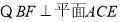
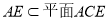
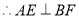 又
又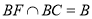
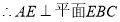
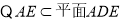
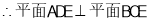 .
.
(2)因為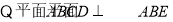
 四棱錐的高即點E到AB的距離,
四棱錐的高即點E到AB的距離,
在直角三角形中ABE中, ,所以,
,所以,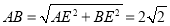 .四棱錐E-ABCD的體積為
.四棱錐E-ABCD的體積為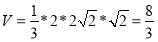 .
.
(3)在三角形ABC過M點作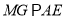 交
交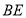 于
于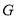 點,在三角形BEC中過G點作
點,在三角形BEC中過G點作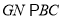 交EC與N點,連MN,則由比例關系易得
交EC與N點,連MN,則由比例關系易得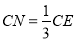 ,
,
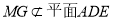
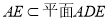
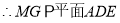 同理,
同理,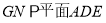
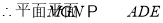 又
又
 N為線段CE上靠近C點的一個三等分點.
N為線段CE上靠近C點的一個三等分點.
考點:空間立體幾何的證明與運算.


科目:高中數學 來源:2015屆江西南昌市四校高二上學期期末聯考文科數學試卷(解析版) 題型:選擇題
有下列四個命題:
①“若 , 則
, 則 互為相反數”的逆命題;
互為相反數”的逆命題;
②“全等三角形的面積相等”的否命題;
③“若 ,則
,則 有實根”的逆否命題;
有實根”的逆否命題;
④“存在 ,使
,使 成立”的否定.
成立”的否定.
其中真命題為( )
A.①② B.②③ C.①③ D.③④
查看答案和解析>>
科目:高中數學 來源:2015屆江蘇省常州市高二上學期期末考試文科數學試卷(解析版) 題型:填空題
“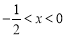 ”是“不等式
”是“不等式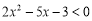 成立”的 條件(在“充分不必要”, “必要不充分”, “充要”, “既不充分又不必要”中選一個填寫).
成立”的 條件(在“充分不必要”, “必要不充分”, “充要”, “既不充分又不必要”中選一個填寫).
查看答案和解析>>
科目:高中數學 來源:2015屆廣東陽東廣雅、陽春實驗中學高二上期末理數學卷(解析版) 題型:選擇題
如圖,在平行六面體ABCD-A1B1C1D1中,底面是邊長為1的正方形,若∠A1AB=∠A1AD=60º,且A1A=3,則A1C的長為( )
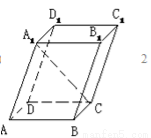
A.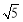 B.
B.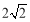 C.
C.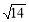 D.
D.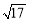
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com