
題目列表(包括答案和解析)
(1)C (2)B (3) D (4)D(5) C (6) A(7)C (8)A (9)C (10)B (11)A (12)D
 (17)(本小題滿分12分)
(17)(本小題滿分12分)
已知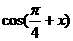 =
=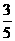 ,求
,求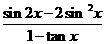 的值.
的值.
 (18)(本小題滿分12分)
(18)(本小題滿分12分)
已知等比數(shù)列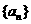 的公比為
的公比為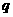 ,前n項(xiàng)的和為
,前n項(xiàng)的和為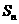 ,且
,且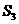 ,
,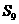 ,
,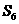 成等差數(shù)列.
成等差數(shù)列.
(Ⅰ)求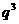 的值;
的值;
(Ⅱ)求證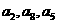 成等差數(shù)列.
成等差數(shù)列.
 (19) (本小題滿分12分)
(19) (本小題滿分12分)
一個(gè)口袋中裝有大小相同的2個(gè)白球和3個(gè)黑球.
(Ⅰ)從中摸出兩個(gè)球,求兩球恰好顏色不同的概率;
(Ⅱ)從中摸出一個(gè)球,放回后再摸出一個(gè)球,求兩球恰好顏色不同的概率.
注意:考生在(20甲)、(20乙)兩題中選一題作答.如果兩題都答,只以(20甲)計(jì)分.
 (20) (本小題滿分12分)
(20) (本小題滿分12分)
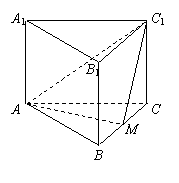 (甲)如圖,正三棱柱
(甲)如圖,正三棱柱 的底面邊長(zhǎng)為
的底面邊長(zhǎng)為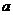 ,點(diǎn)
,點(diǎn)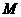 在邊
在邊 上,
上,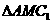 是以點(diǎn)M為直角頂點(diǎn)的等腰直角三角形.
是以點(diǎn)M為直角頂點(diǎn)的等腰直角三角形.
(Ⅰ) 求證點(diǎn)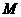 為邊
為邊 的中點(diǎn);
的中點(diǎn);
(Ⅱ) 求點(diǎn) 到平面
到平面 的距離;
的距離;
(Ⅲ) 求二面角 的大小.
的大小.
 (乙) 如圖,直三棱柱ABC-A1B1C1中,底面是以∠ABC為直角的等腰直角三角形,AC=
(乙) 如圖,直三棱柱ABC-A1B1C1中,底面是以∠ABC為直角的等腰直角三角形,AC=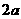 ,BB1=
,BB1=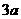 ,D為A1C1的中點(diǎn),E為B1C的中點(diǎn),
,D為A1C1的中點(diǎn),E為B1C的中點(diǎn),
(Ⅰ)求直線BE與A1C所成的角;
(Ⅱ)在線段AA1上是否存在點(diǎn)F,使CF⊥平面B1DF,若存在,求出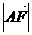 ;若不存在,說(shuō)明理由.
;若不存在,說(shuō)明理由.

(21)(本小題滿分12分)
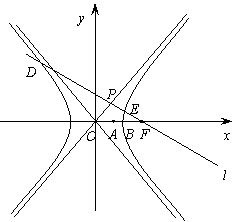 已知雙曲線
已知雙曲線 :
: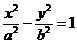
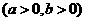 ,
, 是右頂點(diǎn),
是右頂點(diǎn),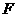 是右焦點(diǎn), 點(diǎn)
是右焦點(diǎn), 點(diǎn) 在
在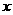 軸正半軸上,且滿足
軸正半軸上,且滿足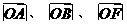 成等比數(shù)列,過(guò)
成等比數(shù)列,過(guò)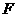 作雙曲線
作雙曲線 在第一、三象限的漸近線的垂線
在第一、三象限的漸近線的垂線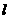 ,垂足為
,垂足為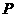 .
.
(Ⅰ)求證: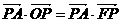 ;
;
(Ⅱ)若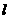 與雙曲線
與雙曲線 的左、右兩支分別相交于點(diǎn)
的左、右兩支分別相交于點(diǎn)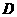 、
、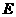 ,求雙曲線
,求雙曲線 的離心率
的離心率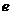 的取值范圍.
的取值范圍.
 (22)(本小題滿分14分)
(22)(本小題滿分14分)
設(shè)函數(shù)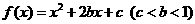 ,
,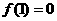 ,且方程
,且方程 +1=0有實(shí)根.
+1=0有實(shí)根.
(Ⅰ)證明: ;
;
(Ⅱ)證明: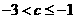 ;
;
(Ⅲ)若 是方程
是方程 +1=0的一個(gè)實(shí)根,判斷
+1=0的一個(gè)實(shí)根,判斷 的正負(fù)并加以證明.
的正負(fù)并加以證明.
高考數(shù)學(xué)模擬試卷2參考解答及評(píng)分標(biāo)準(zhǔn)
說(shuō)明:
(13)若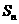 是數(shù)列
是數(shù)列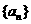 的前
的前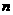 項(xiàng)的和,
項(xiàng)的和,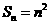 ,則
,則 .
.
(14) 若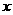 、
、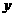 滿足
滿足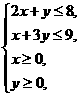 則
則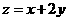 的最大值為
.
的最大值為
.
(15) 有 、
、 、
、 、
、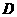 、
、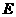 五名學(xué)生參加網(wǎng)頁(yè)設(shè)計(jì)競(jìng)賽,決出了第一到第五的名次,
五名學(xué)生參加網(wǎng)頁(yè)設(shè)計(jì)競(jìng)賽,決出了第一到第五的名次, 、
、 兩位同學(xué)去問(wèn)成績(jī),老師對(duì)
兩位同學(xué)去問(wèn)成績(jī),老師對(duì) 說(shuō):“你沒(méi)能得第一名”.又對(duì)
說(shuō):“你沒(méi)能得第一名”.又對(duì) 說(shuō):“你是第三名”,從這個(gè)問(wèn)題分析,這五人的名次排列共有
種可能(用數(shù)字作答).
說(shuō):“你是第三名”,從這個(gè)問(wèn)題分析,這五人的名次排列共有
種可能(用數(shù)字作答).
(16) 若對(duì)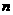 個(gè)向量
個(gè)向量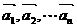 存在
存在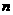 個(gè)不全為零的實(shí)數(shù)
個(gè)不全為零的實(shí)數(shù)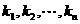 ,使得
,使得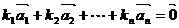 成立,則稱向量
成立,則稱向量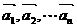 為“線性相關(guān)”.依此規(guī)定,
能說(shuō)明
為“線性相關(guān)”.依此規(guī)定,
能說(shuō)明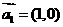 ,
,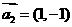 ,
,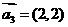 “線性相關(guān)”的實(shí)數(shù)
“線性相關(guān)”的實(shí)數(shù)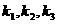 依次可以
依次可以
取 (寫出一組數(shù)值即可,不必考慮所有情況).
四個(gè)選項(xiàng)中,有且只有一項(xiàng)是符合題目要求的.
(1) 設(shè)M和m分別表示函數(shù) 的最大值和最小值,則M+m等于
的最大值和最小值,則M+m等于
(A)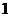 (B)
(B)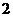 (C)
(C)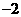 (D)-1
(D)-1
(2) 設(shè)集合M=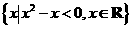 ,N=
,N=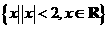 ,則
,則
(A)N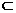 M (B)M
M (B)M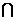 N=M (C)M
N=M (C)M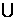 N=M (D)M
N=M (D)M N=
N=
(3) 若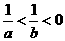 ,則下列結(jié)論不正確的是
,則下列結(jié)論不正確的是
(A)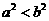 (B)
(B)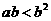 (C)
(C)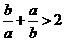 (D)
(D)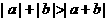
(4) 直線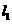 ,
,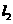 互相平行的一個(gè)充分條件是
互相平行的一個(gè)充分條件是
(A) 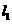 ,
,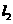 都平行于同一個(gè)平面
(B)
都平行于同一個(gè)平面
(B) 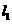 ,
,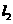 與同一個(gè)平面所成的角相等
與同一個(gè)平面所成的角相等
(C) 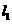 平行于
平行于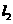 所在的平面
(D)
所在的平面
(D) 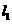 ,
,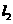 都垂直于同一個(gè)平面
都垂直于同一個(gè)平面
(5) 若二項(xiàng)式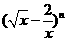 的展開式的第5項(xiàng)是常數(shù)項(xiàng),則自然數(shù)
的展開式的第5項(xiàng)是常數(shù)項(xiàng),則自然數(shù)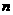 的值為
的值為
(A)6 (B)10 (C)12 (D)15
(6) 已知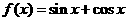 ,則
,則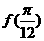 的值為
的值為
(A) 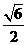 (B)
(B)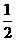 (C)
(C)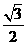 (D)
(D) 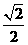
(7) 函數(shù)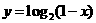 的圖象是
的圖象是
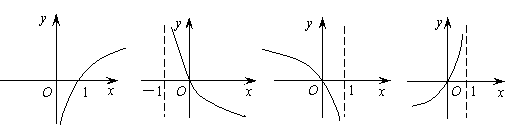 (A)
(B) (C)
(D)
(A)
(B) (C)
(D)
(8)橢圓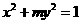 的焦點(diǎn)在
的焦點(diǎn)在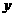 軸上,長(zhǎng)軸長(zhǎng)是短軸長(zhǎng)的兩倍,則
軸上,長(zhǎng)軸長(zhǎng)是短軸長(zhǎng)的兩倍,則 的值為
的值為
(A)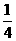 (B)
(B)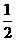 (C)2
(D)4
(C)2
(D)4
(9) 若曲線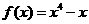 在點(diǎn)P處的切線平行于直線
在點(diǎn)P處的切線平行于直線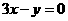 ,則點(diǎn)P的坐標(biāo)為
,則點(diǎn)P的坐標(biāo)為
(A)(1,3) (B)(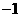 ,3) (C)(1,0) (D)(-1,0)
,3) (C)(1,0) (D)(-1,0)
(10) 已知函數(shù)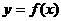 是R上的偶函數(shù),且在
是R上的偶函數(shù),且在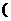
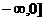 上是減函數(shù),若
上是減函數(shù),若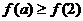 ,則實(shí)數(shù)a的取值范圍是
,則實(shí)數(shù)a的取值范圍是
(A)a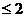 (B) a
(B) a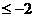 或a
或a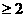 (C) a
(C) a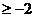 (D)
(D)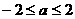
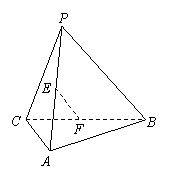 (11)如圖,E、F分別是三棱錐
(11)如圖,E、F分別是三棱錐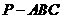 的棱AP、BC的中點(diǎn),
的棱AP、BC的中點(diǎn), 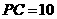 ,
,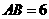 ,EF=7,則異面直線AB與PC所成的角為
,EF=7,則異面直線AB與PC所成的角為
(A) 600 (B)450 (C) 300 (D)1200
(12) 圓心在拋物線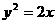 (
(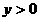 )上,并且與拋物線
)上,并且與拋物線
的準(zhǔn)線及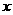 軸都相切的圓的方程是
軸都相切的圓的方程是
(A)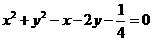 (B)
(B)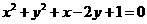
(C)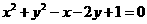 (D)
(D)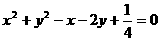
第Ⅱ卷(非選擇題共90分)

22.(本題滿分14分) 已知函數(shù)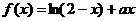 在開區(qū)間(0,1)內(nèi)是增函數(shù).
在開區(qū)間(0,1)內(nèi)是增函數(shù).
(Ⅰ) 求實(shí)數(shù)a的取值范圍;
(Ⅱ) 若數(shù)列{an}滿足a1∈(0,1),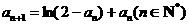 ,證明:
,證明: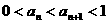 .
.
(Ⅲ) 若數(shù)列{bn}滿足b1∈(0,1),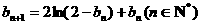 ,問(wèn)數(shù)列{bn}是否單調(diào)?
,問(wèn)數(shù)列{bn}是否單調(diào)?
(Ⅰ) 解: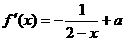 ,由于f (x)在(0,1)內(nèi)是增函數(shù),
,由于f (x)在(0,1)內(nèi)是增函數(shù),
∴ 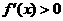 ,即
,即 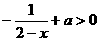 在x∈(0,1)時(shí)恒成立.
在x∈(0,1)時(shí)恒成立.
∴ 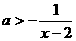 恒成立,
恒成立,
而 -2<x-2<-1,
∴ 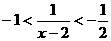 ,
,
即 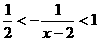 ,
,
∴ a≥1即為所求.
(Ⅱ) 證明:由題設(shè)知,當(dāng)n=1時(shí),a1∈(0,1).
假設(shè)當(dāng)n=k時(shí),有ak∈(0,1),則
當(dāng)n=k+1時(shí),有 且
且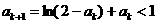 (由第一問(wèn)知f(x)=ln(2-x)+x在(0,1)上是增函數(shù)),
(由第一問(wèn)知f(x)=ln(2-x)+x在(0,1)上是增函數(shù)),
∴ n=k+1時(shí)命題成立,故0<an<1,n∈N*.
又 ∵ 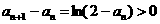 ,
,
∴ 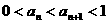 .
.
(Ⅲ) 數(shù)列{bn}不具有單調(diào)性.
令 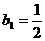 , 則
, 則 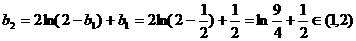 ,
,
∴ b2>b1.
又 ∵ 1<b2<2,0<2-b2<1,
∴ ln(2-b2)<0,
∴ 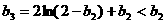 .
.
由此表明數(shù)列{bn}沒(méi)有單調(diào)性.
21.(本題滿分12分) 某保險(xiǎn)公司新開設(shè)了一項(xiàng)保險(xiǎn)業(yè)務(wù),若在一年內(nèi)事件E發(fā)生,該公司要賠償a元.設(shè)在一年內(nèi)E發(fā)生的概率為p,為使公司收益的期望值等于a的百分之十,公司應(yīng)要求顧客交多少保險(xiǎn)金?
解:設(shè)保險(xiǎn)公司要求顧客交x元保險(xiǎn)金,若以x表示公司每年的收益額,則x是一個(gè)隨機(jī)變量,其分布列為:
|
x |
x |
x-a |
|
P |
1-p |
p |
因此,公司每年收益的期望值為
Ex=x(1-p)+(x-a)·p=x-ap.
為使公司收益的期望值等于a的百分之十,
只需Ex=0.1a,即x-ap=0.1a,
故可得x=(0.1+p)a.
即顧客交的保險(xiǎn)金為(0.1+p)a時(shí),可使公司期望獲益10%a.
說(shuō)明:當(dāng)事件E發(fā)生的概率較小時(shí),即使賠償數(shù)目較大,保險(xiǎn)公司仍可獲益.例如當(dāng)P=0.001,a=10000元時(shí),根據(jù)上述賠償辦法,顧客只需交納(0.1+0.001)×10000=1010元保險(xiǎn)金,但保險(xiǎn)公司仍可期望獲益10%a=1000元,當(dāng)保險(xiǎn)公司的顧客較多時(shí),其效益十分可觀.
20.(本題滿分12分) 已知f(x)是定義在(-∞,0)∪(0,+∞)上的奇函數(shù),當(dāng)x<0時(shí),f(x)=x2-x-2,解不等式f(x)>0.
解: 設(shè)x>0,則 -x<0.
∴ f (-x)=(-x)2-(-x)-2=x2+x-2.
而f (x) 是奇函數(shù),
∴ f (-x)=-f (x),
于是 f (x)=-x2-x+2,x>0.
∴ 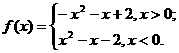
(1) 由 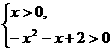 得
得 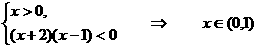 .
.
(2) 由 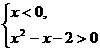 得
得 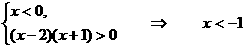 .
.
綜上所述,不等式f (x)>0的解集為{x∣x<-1或0<x<1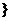 .
.
19.(本題滿分12分) 已知p:∣1-2x∣≤ 5,q:x2-4x+4-9m2 ≤ 0 (m>0),若 p是
p是 q的充分而不必要條件,求實(shí)數(shù)m的取值范圍.
q的充分而不必要條件,求實(shí)數(shù)m的取值范圍.
解:解不等式可求得:
p:-2≤x≤3, q:2-3m≤x≤2+3m (m>0).
則  p:A={x∣x<-2或x>3},
p:A={x∣x<-2或x>3},
 q:B={x∣x<2-3m或x>2+3m,m>0
q:B={x∣x<2-3m或x>2+3m,m>0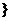 .
.
由已知  p
p 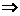
 q,得A
q,得A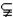 B,從而
B,從而
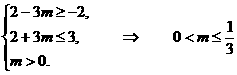 .
.
(上述不等式組中等號(hào)不能同時(shí)取).
經(jīng)驗(yàn)證 為所求實(shí)數(shù)m的取值范圍.
為所求實(shí)數(shù)m的取值范圍.
18.(本題滿分12分) 已知函數(shù)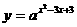 在[0,2]上有最小值8,求正數(shù)a的值.
在[0,2]上有最小值8,求正數(shù)a的值.
解:設(shè)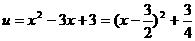 ,
,
當(dāng)x∈[0,2]時(shí),可得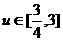 .
.
(1) 若a>1時(shí),則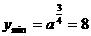 ,解得a=16>1.
,解得a=16>1.
(2) 若0<a<1時(shí),則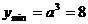 ,解得a=2,此與0<a<1矛盾,舍去.
,解得a=2,此與0<a<1矛盾,舍去.
故正數(shù)a =16.
17.解: (Ⅰ) 由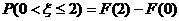 =
=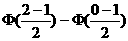
=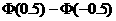 =2
=2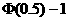
=2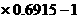 =0.3830.
=0.3830.
(Ⅱ) 由已知可得 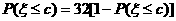 ,
,
∴ 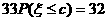 ,
,
即 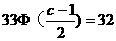 ,
,
∴ 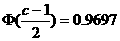 ,
,
∴ 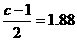 , c=4.76.
, c=4.76.
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com