中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 初中數學 > 題目詳情

如圖，一次函數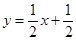的圖象與x軸交于點A，與y軸交于點B，與反比例函數的圖象在第一象限內交于點C，CD⊥x軸于點D，OD＝2AO，求反比例函數的表達式．

.

解析試題分析：根據已知，應用相似三角形的判定和性質以及曲線上點的坐標與方程的關系求出點C的坐標，代入即可求解.
∵一次函數的圖象與x軸交于點A，與y軸交于點B ，
∴令，得；令，得.
∴點A坐標為，點B坐標為. ∴OA=1，OB=.
∵CD⊥x軸，∴CD//OB. △AOB∽△ADC. .
∵OD=2AO，. ∴CD=.
∴點C的縱坐標為.
∵點C在一次函數的圖象上，∴點C的坐標為.
∴反比例函數的表達式 .
考點：1.一次函數與反比例函數交點問題；2.曲線上點的坐標與方程的關系；3.相似三角形的判定和性質.

練習冊系列答案
相關習題

科目：初中數學 來源： 題型：解答題

關于x的函數y=（m2-1）x2-（2m+2）x+2的圖象與x軸只有一個公共點，求m的值．

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

為了響應國家節能減排的號召，鼓勵市民節約用電，我市從2012年7月1日起，居民用電實行“一戶一表”的“階梯電價”，分三個檔次收費，第一檔是用電量不超過180千瓦時實行“基本電價”，第二、三檔實行“提高電價”，具體收費情況如圖的折線圖，請根據圖象回答下列問題；
(1)當用電量是180千瓦時時，電費是__________元；
(2)第二檔的用電量范圍是__________；
(3)“基本電價”是__________元/千瓦時；
(4)小明家8月份的電費是328．5元，這個月他家用電多少千瓦時？

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

如圖，在平面直角坐標系中，直線y＝2x＋b（b＜0）與坐標軸交于A，B兩點，與雙曲線（x>0）交于D點，過點D作DC⊥x軸，垂足為C，連接OD。已知△AOB≌△ACD。
（1）如果b=－2，求k的值；
（2）試探究k與b的數量關系，并寫出直線OD的解析式。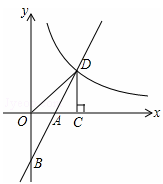

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

已知A、B兩地相距300千米，甲、乙兩車同時從A地出發，以各自的速度勻速往返兩地，甲車先到達B地，停留1小時后按原路返回．設兩車行駛的時間為x小時，離開A地的距離是y千米，如圖是y與x的函數圖象．
(1)計算甲車的速度為   千米／時，乙車的速度為   千米／時；
(2)幾小時后兩車相遇；
(3)在從開始出發到兩車相遇的過程中，設兩車之間的距離為S千米，乙車行駛的時間為t小時，求S與t之間的函數關系式．

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

某移動通訊公司開設了兩種通訊業務：“全球通”使用者先繳50元月租費，然后每通話1分鐘，再付話費0．4元；“神舟行”不繳月租費，每通話1min付費0．6元．若一個月內通話x min，兩種方式的費用分別為y1元和y2元．
（1）寫出y1、y2與x之間的函數關系式；
（2）一個月內通話多少分鐘，兩種移動通訊費用相同；
（3）你能為用戶設計一個方案，使用戶合理地選擇通信業務嗎？
（4）某人估計一個月內通話300min，應選擇哪種移動通訊合算些．

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

在學習三角形中線的知識時，小明了解到：三角形的任意一條中線所在的直線可以把該三角形分為面積相等的兩部分。進而，小明繼續研究，過四邊形的某一頂點的直線能否將該四邊形平分為面積相等的兩部分？他畫出了如下示意圖（如圖1），得到了符合要求的直線AF.

小明的作圖步驟如下：
第一步：連結AC；
第二步：過點B作BE//AC交DC的延長線于點E；
第三步：取ED中點F，作直線AF；
則直線AF即為所求.
請參考小明思考問題的方法，解決問題：
如圖2，五邊形ABOCD，各頂點坐標為：A(3,4)，B(0,2)，O(0,0)，C(4,0)，D(4,2).請你構造一條經過頂點A的直線，將五邊形ABOCD分為面積相等的兩部分，并求出該直線的解析式.

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

某公司有甲種原料260kg，乙種原料270kg，計劃用這兩種原料生產A、B兩種產品共40件．生產每件A種產品需甲種原料8kg，乙種原料5kg，可獲利潤900元；生產每件B種產品需甲種原料4kg，乙種原料9kg，可獲利潤1100元．設安排生產A種產品x件．
（1）完成下表

 
甲（kg）
乙（kg）
件數（件）
A
 
5x
x
B
4（40-x）
 
40-x
（2）安排生產A、B兩種產品的件數有幾種方案？試說明理由；
（3）設生產這批40件產品共可獲利潤y元，將y表示為x的函數，并求出最大利潤．

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

如圖，直線y=k1x+b（k1≠0）與雙曲線（k2≠0）相交于A（1，m）、B（-2，-1）兩點．求直線和雙曲線的解析式．

查看答案和解析>>

同步練習冊答案