
在氣候對人類生存壓力日趨加大的今天,發展低碳經濟,全面實現低碳生活成為人們的共識,某企業采用技術革新,節能減排,經分析前5個月二氧化碳排放量y(噸)與月份x(月)之間的函數關系是y=-2x+50.
(1)隨著二氧化碳排放量的減少,每排放一噸二氧化碳,企業相應獲得的利潤也有所提高,且相應獲得的利潤p(萬元)與月份x(月)的函數關系如圖所示,那么哪月份,該企業獲得的月利潤最大?最大月利潤是多少萬元?
(2)受國家政策的鼓勵,該企業決定從6月份起,每月二氧化碳排放量在上一個月的基礎上都下降a%,與此同時,每排放一噸二氧化碳,企業相應獲得的利潤在上一個月的基礎上都增加50%,要使今年6、7月份月利潤的總和是今年5月份月利潤的3倍,求a的值(精確到個位).
(參考數據: =7.14,
=7.14, =7.21,
=7.21, =7.28,
=7.28,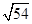 =7.35)
=7.35)
(1)5,4000;(2)13.
解析試題分析:(1)根據圖象可以知道利潤p(萬元)與月份x是一次函數關系,并且隨著月份的增加利潤也增加,首先根據圖象確定利潤p與x的函數關系,然后利用函數的增減性即可確定今年哪月份,該企業獲得的月利潤最大?最大月利潤是多少萬元;
(2)由于該企業決定從今年6月份起,每月二氧化碳排放量在上一個月的基礎上都下降a%,與此同時,每排放一噸二氧化碳,企業相應獲得的利潤在上一個月的基礎上都增加50%.
試題解析:(1)根據圖象知道當x=1,p=80,
當x=4,p=95,
設p=kx+b,
∴  ,解得
,解得 ,
,
∴p=5x+75;根據k>0,y隨x增大而增大,
∴當x=5時,p最大,p=5×5+75=100萬元;
∴5月份的利潤是:100萬×40=4000萬元;
(2)(2)∵該企業決定從今年6月份起,每月二氧化碳排放量在上一個月的基礎上都下降a%,
而當x=5時,y=40,
∴6月份的二氧化碳排放量為40(1-a%),
7月份的二氧化碳排放量為40(1-a%)2,
5月份的利潤為4000萬元,
∴6月份的利潤為100(1+50%)×40(1-a%),
7月份的利潤為100(1+50%)×(1+50%)×40(1-a%)2,
∴100(1+50%)×40(1-a%)+100(1+50%)×(1+50%)×40(1-a%)2=3×4000,
∴a=13.
考點:二次函數的應用.


科目:初中數學 來源: 題型:解答題
已知關于 的方程:
的方程: ①和
①和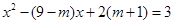 ②,其中
②,其中 .
.
(1)求證:方程①總有兩個不相等的實數根;
(2)設二次函數 的圖象與
的圖象與 軸交于
軸交于 、
、 兩點(點
兩點(點 在點
在點 的左側),將
的左側),將 、
、 兩點按照相同的方式平移后,點
兩點按照相同的方式平移后,點 落在點
落在點 處,點
處,點 落在點
落在點 處,若點
處,若點 的橫坐標恰好是方程②的一個根,求
的橫坐標恰好是方程②的一個根,求 的值;
的值;
(3)設二次函數 ,在(2)的條件下,函數
,在(2)的條件下,函數 ,
, 的圖象位于直線
的圖象位于直線 左側的部分與直線
左側的部分與直線 (
( )交于兩點,當向上平移直線
)交于兩點,當向上平移直線 時,交點位置隨之變化,若交點間的距離始終不變,則
時,交點位置隨之變化,若交點間的距離始終不變,則 的值是________________.
的值是________________.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,拋物線y=-x2+bx+c與x軸交于A、B兩點,與y軸交于點C,點O為坐標原點,點D為拋物線的頂點,點E在拋物線上,點F在x軸上,四邊形OCEF為矩形,且OF=2,EF=3,
(1)求拋物線所對應的函數解析式;
(2)求△ABD的面積;
(3)將△AOC繞點C逆時針旋轉90°,點A對應點為點G,問點G是否在該拋物線上?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
在平面直角坐標系xOy中,直線 分別與x軸,y軸交于過點A,B,點C是第一象限內的一點,且AB=AC,AB⊥AC,拋物線
分別與x軸,y軸交于過點A,B,點C是第一象限內的一點,且AB=AC,AB⊥AC,拋物線 經過A,C兩點,與
經過A,C兩點,與 軸的另一交點為D.
軸的另一交點為D.
(1)求此拋物線的解析式;
(2)判斷直線AB與CD的位置關系,并證明你的結論;
(3)點M為x軸上一動點,在拋物線上是否存在一點N,使以A,B,M,N四點構成的四邊形為平行四邊形?若存在,求點N的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知某商品的進價為每件40元,售價是每件60元,每星期可賣出300件。市場調查反映:如調整價格 ,每漲價一元,每星期要少賣出10件。該商品應定價為多少元時,商場能獲得最大利潤?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖1,把邊長分別是為4和2的兩個正方形紙片OABC和OD′E′F′疊放在一起.
(1)操作1:固定正方形OABC,將正方形OD′E′F′繞點O按順時針方向旋轉45°得到正方形ODEF,如圖2,連接AD、CF,線段AD與CF之間有怎樣的數量關系?試證明你的結論;
(2)操作2,如圖2,將正方形ODEF沿著射線DB以每秒1個單位的速度平移,平移后的正方形ODEF設為正方形PQMN,如圖3,設正方形PQMN移動的時間為x秒,正方形PQMN與正方形OABC的重疊部分面積為y,直接寫出y與x之間的函數解析式;
(3)操作3:固定正方形OABC,將正方形OD′E′F′繞點O按順時針方向旋轉90°得到正方形OHKL,如圖4,求△ACK的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖所示,二次函數y=-x2+2x+m的圖象與x軸的一個交點為A(3,0),另一個交點為B,且與y軸交于點C.
(1)求m的值;
(2)求點B的坐標;
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在平面直角坐標系xOy中,一次函數y= x+m (m為常數)的圖像與x軸交于點A(-3,0),與y軸交于點C.以直線x=1為對稱軸的拋物線y=ax2+bx+c(a,b,c為常數,且a≠0)經過A、C兩點,并與x軸的正半軸交于點B.
x+m (m為常數)的圖像與x軸交于點A(-3,0),與y軸交于點C.以直線x=1為對稱軸的拋物線y=ax2+bx+c(a,b,c為常數,且a≠0)經過A、C兩點,并與x軸的正半軸交于點B.
(1)求m的值及拋物線的函數表達式;
(2)若P是拋物線對稱軸上一動點,△ACP周長最小時,求出P的坐標;
(3)是否存在拋物在線一動點Q,使得△ACQ是以AC為直角邊的直角三角形?若存在,求出點Q的橫坐標;若不存在,請說明理由;
(4)在(2)的條件下過點P任意作一條與y軸不平行的直線交拋物線于M1(x1,y1),M2(x2,y2)兩點,試問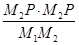 是否為定值,如果是,請直接寫出結果,如果不是請說明理由.
是否為定值,如果是,請直接寫出結果,如果不是請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com