Question

已知, BC∥OA，∠B=∠A=100°，試回答下列問題：
如圖1所示，求證：OB∥AC.
（2）如圖2，若點E、F在線段BC上，且滿足∠FOC=∠AOC ，并且OE平分∠BOF.則∠EOC的度數等于__     _____；(在橫線上填上答案即可）.
（3）在（2） 的條件下，若平行移動AC，如圖3，那么∠OCB:∠OFB的值是否隨之發生變化？若變化，試說明理由；若不變，求出這個比值.
（4）在（3）的條件下，如果平行移動AC的過程中，若使∠OEB=∠OCA，此時∠OCA度數等于             .（在橫線上填上答案即可）.  

Answer 1

(1)證明見試題解析；（2）40⁰；（3）不變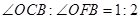，；（4）60^0.

解析試題分析：（1）根據等式性質及平行線的判定可以得到證明思路.(2)根據角平分線及觀察圖形知道
∠EOC=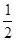∠BOC=40⁰.(3)∠OFB與∠OCB實際上是三角形的外角與不相鄰的內角的關系，再觀察圖形可知兩直線平行內錯角相等，角平分線分得的兩個角相等，等量代換可得結論.（4）由∠OEB=∠OCA可以推出∠BOE=∠BCO=∠EOF=∠COF∠COA=20⁰，從而∠OCA=60⁰.
試題解析：
（1）∵∴
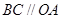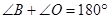
又∵∴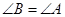
∴
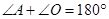
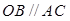
(2)40°
（3）∵
∴
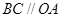
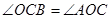
又∵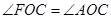
∴
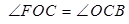
又∵∴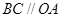
∴
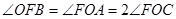
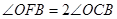
即
(4)60°
考點：1平行線的判定性質;2三角形的內外角關系;3角平分線性質;4等式性質.