
剖析:由雙曲線中心在原點,準線平行于x軸,可設雙曲線的方程為![]() -
-![]() =1.
=1.
由離心率為![]() ,可得a2+b2=(
,可得a2+b2=(![]() a)2=c2.
a)2=c2.
由點P(0,5)到此雙曲線上的點的最近距離為2,可轉化為二次函數的最大(小)值問題來討論,得到a、b應滿足的另一關系式.從而求出a2、b2,本題得解.
解:依題意,設雙曲線的方程為![]() -
-![]() =1(a>0,b>0).
=1(a>0,b>0).
∵e=![]() =
=![]() ,c2=a2+b2,
,c2=a2+b2,
∴a2=4b2.
設M(x,y)為雙曲線上任一點,則
|PM|2=x2+(y-5)2
=b2(![]() -1)+(y-5)2
-1)+(y-5)2
=![]() (y-4)2+5-b2(|y|≥2b).
(y-4)2+5-b2(|y|≥2b).
①若4≥2b,則當y=4時,
|PM|min2=5-b2=4,得b2=1,a2=4.
從而所求雙曲線方程為![]() -x2=1.
-x2=1.
②若4<2b,則當y=2b時,
|PM|min2=4b2-20b+25=4,
得b=![]() (舍去b=
(舍去b=![]() ),b2=
),b2=![]() ,a2=49.
,a2=49.
從而所求雙曲線方程為![]() -
-![]() =1.
=1.


 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:高中數學 來源:2006年高考第一輪復習數學:8.2 雙曲線(解析版) 題型:解答題
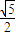 ,且點P(0,5)到此雙曲線上的點的最近距離為2,求雙曲線的方程.
,且點P(0,5)到此雙曲線上的點的最近距離為2,求雙曲線的方程.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com