
在平面直角坐標(biāo)系內(nèi)已知兩點(diǎn)A(-1,0)、B(1,0),若將動(dòng)點(diǎn)P(x,y)的橫坐標(biāo)保持不變,縱坐標(biāo)擴(kuò)大到原來(lái)的 倍后得到點(diǎn)Q(x,
倍后得到點(diǎn)Q(x, y),且滿足
y),且滿足 ·
· =1.
=1.
(Ⅰ)求動(dòng)點(diǎn)P所在曲線C的方程;
(Ⅱ)過(guò)點(diǎn)B作斜率為- 的直線l交曲線C于M、N兩點(diǎn),且
的直線l交曲線C于M、N兩點(diǎn),且 +
+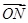 +
+ =
= ,試求△MNH的面積.
,試求△MNH的面積.
(1)曲線C的方程是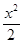 + y2=1 (2)S=
+ y2=1 (2)S=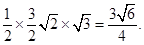
【解析】(I) 設(shè)點(diǎn)P的坐標(biāo)為(x,y),則點(diǎn)Q的坐標(biāo)為(x,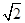 y).然后求出
y).然后求出 =(x+1,
=(x+1,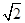 y),
y), 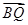 =(x-1,
=(x-1,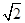 y). 再對(duì)
y). 再對(duì) ·
·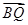 =1坐標(biāo)化化簡(jiǎn)即可。
=1坐標(biāo)化化簡(jiǎn)即可。
(II)先求出直線l的方程,然后與曲線C的方程聯(lián)立,消去y,得到關(guān)于x的一元二次方程。
下面解題的關(guān)鍵是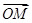 +
+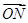 +
+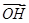 =
=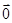 ,得
,得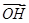 =(- x1- x2,- y1- y2),即H(-1,-
=(- x1- x2,- y1- y2),即H(-1,-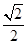 )
)
|MN|=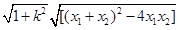 然后利用韋達(dá)定理求出|MN|,再利用點(diǎn)到直線的距離公式求出高,問(wèn)題得解。
然后利用韋達(dá)定理求出|MN|,再利用點(diǎn)到直線的距離公式求出高,問(wèn)題得解。
解:(Ⅰ)設(shè)點(diǎn)P的坐標(biāo)為(x,y),則點(diǎn)Q的坐標(biāo)為(x,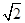 y).
y).
依據(jù)題意,有 =(x+1,
=(x+1,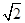 y),
y), 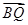 =(x-1,
=(x-1,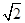 y).
………………2分
y).
………………2分
∵ ·
·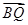 =1,∴x2-1+2 y2=1.∴動(dòng)點(diǎn)P所在曲線C的方程是
=1,∴x2-1+2 y2=1.∴動(dòng)點(diǎn)P所在曲線C的方程是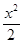 + y2=1 …………4分
+ y2=1 …………4分
(Ⅱ)因直線l過(guò)點(diǎn)B,且斜率為k=-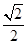 ,故有l(wèi)∶y=-
,故有l(wèi)∶y=-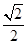 (x-1)………………5分
(x-1)………………5分
聯(lián)立方程組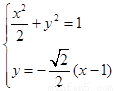 ,消去y,得2x2-2x-1=0.
…………………7分
,消去y,得2x2-2x-1=0.
…………………7分
設(shè)M(x1,y1)、N(x2,y2),可得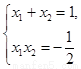 ,于是
,于是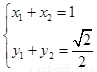 . ……………8分
. ……………8分
又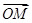 +
+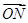 +
+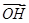 =
=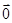 ,得
,得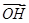 =(- x1- x2,- y1-
y2),即H(-1,-
=(- x1- x2,- y1-
y2),即H(-1,-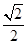 )……10分
)……10分
∴|MN|=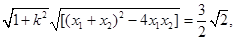 …………………………………12分
…………………………………12分
又l: 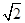 x+2y-
x+2y-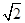 =0,則H到直線l的距離為d=
=0,則H到直線l的距離為d=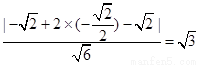
故所求MNH三角形的面積為S=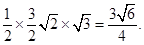


 課時(shí)訓(xùn)練江蘇人民出版社系列答案
課時(shí)訓(xùn)練江蘇人民出版社系列答案 黃岡經(jīng)典趣味課堂系列答案
黃岡經(jīng)典趣味課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
| 2 |
| 2 |
| AQ |
| BQ |
| ||
| 2 |
| OM |
| ON |
| OH |
| 0 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
| 2 |
| 2 |
| AQ |
| BQ |
| ||
| 2 |
| OM |
| ON |
| OH |
| 0 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2013屆廣東省高二下期中理科數(shù)學(xué)試卷(解析版) 題型:解答題
(本小題滿分14分)
在平面直角坐標(biāo)系內(nèi)已知兩點(diǎn)A(-1,0)、B(1,0),若將動(dòng)點(diǎn)P(x,y)的橫坐標(biāo)保持不變,縱坐標(biāo)擴(kuò)大到原來(lái)的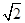 倍后得到點(diǎn)Q(x,
倍后得到點(diǎn)Q(x,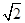 y),且滿足
y),且滿足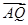 ·
· =1.
=1.
(1)求動(dòng)點(diǎn)P所在曲線C的方程;
(2)過(guò)點(diǎn)B作斜率為- 的直線L交曲線C于M、N兩點(diǎn),且
的直線L交曲線C于M、N兩點(diǎn),且 +
+ +
+ =
=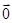 ,試求△MNH的面積.
,試求△MNH的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2012年山東省萊蕪一中高三4月自主檢測(cè)數(shù)學(xué)試卷(文科)(解析版) 題型:解答題
 倍后得到點(diǎn)Q(x,
倍后得到點(diǎn)Q(x, y),且滿足
y),且滿足 •
• =1.
=1. 的直線l交曲線C于M、N兩點(diǎn),且
的直線l交曲線C于M、N兩點(diǎn),且 +
+ +
+ =
= ,試求△MNH的面積.
,試求△MNH的面積.查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com