
對于在區間 [ m,n ] 上有意義的兩個函數 與
與 ,如果對任意
,如果對任意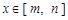 ,均有
,均有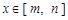 ,則稱
,則稱 與
與 在 [ m,n ] 上是友好的,否則稱
在 [ m,n ] 上是友好的,否則稱 與
與 在 [ m,n ]是不友好的.現有兩個函數
在 [ m,n ]是不友好的.現有兩個函數 與
與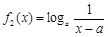 (a > 0且
(a > 0且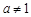 ),給定區間
),給定區間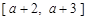 .
.
(1)若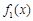 與
與 在給定區間
在給定區間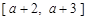 上都有意義,求a的取值范圍;
上都有意義,求a的取值范圍;
(2)討論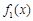 與
與 在給定區間
在給定區間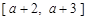 上是否友好.
上是否友好.
(1) 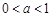 ;(2) 當
;(2) 當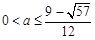 時,
時,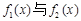 在
在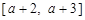 上是友好的,當
上是友好的,當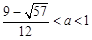 時,
時,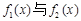 在
在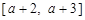 上是不友好的
上是不友好的
解析試題分析:(1)函數f(x)與g(x)在區間[a+2,a+3]上有意義,必須滿足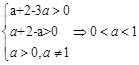 (2)假設存在實數a,使得函數f(x)與g(x)在區間[a+2,a+3]上是“友好”的,
(2)假設存在實數a,使得函數f(x)與g(x)在區間[a+2,a+3]上是“友好”的,
則|f(x)-g(x)|=|loga(x2-4ax+3a2)|⇒|loga(x2-4ax+3a2)|≤1即-1≤loga(x2-4ax+3a2)≤1(*),因為a∈(0,1)⇒2a∈(0,2),而[a+2,a+3]在x=2a的右側,
所以函數g(x)=loga(x2-4ax+3a2)在區間[a+2,a+3]上為減函數,從而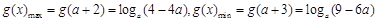 ,于是不等式(*)成立的充要條件是
,于是不等式(*)成立的充要條件是 ,因此,當
,因此,當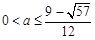 時,
時,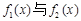 在
在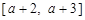 上是友好的; 當
上是友好的; 當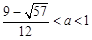 時,
時,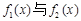 在
在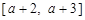 上是不友好的
上是不友好的
考點:本題考查了函數的定義域及單調性
點評:此類問題要求學生熟練掌握函數單調性的判斷與證明,以及新定義的運用,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
提高過江大橋的車輛通行能力可改善整個城市的交通狀況.在一般情況下,大橋上的車流速度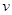 (單位:千米/小時)是車流密度
(單位:千米/小時)是車流密度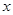 (單位:輛/千米)的函數.當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0千米/小時;當車流密度不超過20輛/千米時,車流速度為60千米/小時.研究表明:當
(單位:輛/千米)的函數.當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0千米/小時;當車流密度不超過20輛/千米時,車流速度為60千米/小時.研究表明:當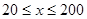 時,車流速度
時,車流速度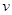 是車流密度
是車流密度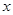 的一次函數.
的一次函數.
(Ⅰ)當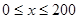 時,求函數
時,求函數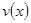 的表達式;
的表達式;
(Ⅱ)當車流密度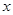 為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)
為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)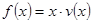 可以達到最大,并求出最大值.(精確到1輛/小時).
可以達到最大,并求出最大值.(精確到1輛/小時).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=ax2+2x+c(a、c∈N*)滿足:①f(1)=5;②6<f(2)<11.
(1)求a、c的值;
(2)若對任意的實數x∈ ,都有f(x)-2mx≤1成立,求實數m的取值范圍.
,都有f(x)-2mx≤1成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數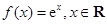 .
.
(Ⅰ) 若直線y=kx+1與f (x)的反函數的圖像相切, 求實數k的值;
(Ⅱ) 設x>0, 討論曲線y=f (x) 與曲線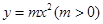 公共點的個數.
公共點的個數.
(Ⅲ) 設a<b, 比較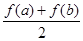 與
與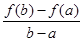 的大小, 并說明理由.
的大小, 并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數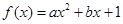 (
(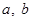 為實數,
為實數,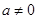 ,
,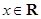 ),
),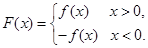
(Ⅰ)若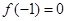 ,且函數
,且函數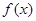 的值域為
的值域為 ,求
,求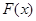 的表達式;
的表達式;
(Ⅱ)在(Ⅰ)的條件下,當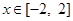 時,
時, 是單調函數,求實數
是單調函數,求實數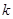 的取值范圍;
的取值范圍;
(Ⅲ)設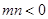 ,
,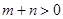 ,
,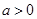 ,且函數
,且函數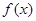 為偶函數,判斷
為偶函數,判斷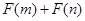 是否大于
是否大于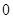 ?
?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=lg(ax-bx)(a>1>b>0).
(1)求y=f(x)的定義域;
(2)在函數y=f(x)的圖象上是否存在不同的兩點,使得過這兩點的直線平行于x軸;
(3)當a,b滿足什么條件時,f(x)在(1,+∞)上恒取正值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某人2002年底花100萬元買了一套住房,其中首付30萬元,70萬元采用商業貸款.貸款的月利率為5‰,按復利計算,每月等額還貸一次,10年還清,并從貸款后的次月開始還貸.
(1)這個人每月應還貸多少元?
(2)為了抑制高房價,國家出臺“國五條”,要求賣房時按照差額的20%繳稅.如果這個人現在將住房150萬元賣出,并且差額稅由賣房人承擔,問:賣房人將獲利約多少元?(參考數據:(1+0.005)120≈1.8)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com