
(本小題滿分16分)
已知數列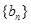 滿足
滿足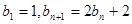 ,
,
(1)求證:數列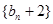 為等比數列 (2)求數列
為等比數列 (2)求數列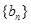 的通項公式
的通項公式
(3)試問:數列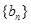 中是否存在不同的三項恰好成等差數列?若存在,求出這三項;若不存在,請說明理由.
中是否存在不同的三項恰好成等差數列?若存在,求出這三項;若不存在,請說明理由.
(1) ∵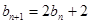 ,∴
,∴
所以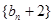 是以
是以 為首項,2為公比的等比數列....5分
為首項,2為公比的等比數列....5分
(2) 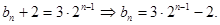 ...........10分
...........10分
(3)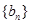 中不存在不同的三項
中不存在不同的三項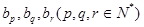 恰好成等差數列.
恰好成等差數列.
【解析】
試題分析:(1)由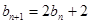 ,得
,得 ,
,
根據等比數列的定義可知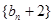 是等比數列.
是等比數列.
(2)在(1)的基礎上,可求出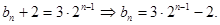
(3)解本小題的關鍵:假設數列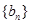 中存在不同的三項
中存在不同的三項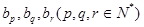 恰好成等差數列,顯然
恰好成等差數列,顯然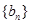 是遞增數列,然后可設
是遞增數列,然后可設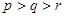 ,則
,則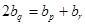 即
即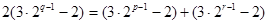 ,進而得到
,進而得到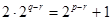 ,
,
然后再根據p,q,r取正整數值,并且還要從奇偶性判斷是否存在.
(1) ∵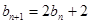 ,∴
,∴
所以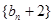 是以
是以 為首項,2為公比的等比數列....5分
為首項,2為公比的等比數列....5分
(2) 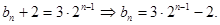 ...........10分
...........10分
(3)若數列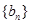 中存在不同的三項
中存在不同的三項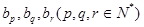 恰好成等差數列,顯然
恰好成等差數列,顯然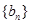 是遞增數列,不妨設
是遞增數列,不妨設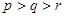 ,則
,則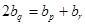
即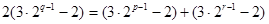 ,化簡得:
,化簡得:
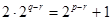 ……(*)................14分
……(*)................14分
由于 ,且
,且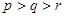 ,知
,知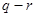 ≥1,
≥1,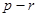 ≥2,
≥2,
所以(*)式左邊為偶數,右邊為奇數,
故數列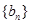 中不存在不同的三項
中不存在不同的三項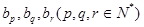 恰好成等差數列..16分
恰好成等差數列..16分
考點:等比數列的定義,與數列有關的探究性問題.
點評:等比數列的定義是判定一個數列是否是等比數列的依據,勿必理解掌握.對于探索性問題可先假設存在,然后根據條件探索存在應滿足的條件,從而最終得出結論.


科目:高中數學 來源:2014屆江蘇連云港灌南高級中學高二上期中考試文數學試卷(解析版) 題型:解答題
(本小題滿分16分)
已知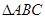 外接圓的半徑為2,
外接圓的半徑為2,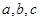 分別是
分別是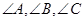 的對邊
的對邊
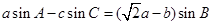
(1)求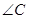 (2)求
(2)求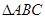 面積的最大值
面積的最大值
查看答案和解析>>
科目:高中數學 來源:2014屆江蘇連云港灌南高級中學高二上期中考試文數學試卷(解析版) 題型:解答題
(本小題滿分16分)
已知二次函數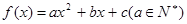 ,若不等式
,若不等式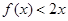 的解集為
的解集為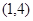 ,且方程
,且方程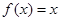 有兩個相等的實數根.(1)求
有兩個相等的實數根.(1)求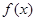 的解析式;(2)若不等式
的解析式;(2)若不等式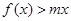 在
在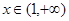 上恒成立,求實數
上恒成立,求實數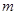 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江蘇省蘇北四市(徐、連、淮、宿)高三元月調研測試數學試卷 題型:解答題
(本小題滿分16分)設數列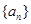 的前n項和為
的前n項和為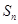 ,已知
,已知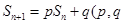 為常數,
為常數,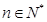 ),eg
),eg 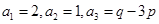
(1)求p,q的值;
(2)求數列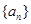 的通項公式;
的通項公式;
(3)是否存在正整數m,n,使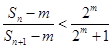 成立?若存在,求出所有符合條件的有序實數對(m,n);若不存在,說明理由。
成立?若存在,求出所有符合條件的有序實數對(m,n);若不存在,說明理由。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江蘇省蘇北四市(徐、連、淮、宿)高三元月調研測試數學試卷 題型:解答題
(本小題滿分16分)平面直角坐標系xoy中,直線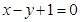 截以原點O為圓心的圓所得的弦長為
截以原點O為圓心的圓所得的弦長為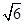
(1)求圓O的方程;
(2)若直線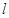 與圓O切于第一象限,且與坐標軸交于D,E,當DE長最小時,求直線
與圓O切于第一象限,且與坐標軸交于D,E,當DE長最小時,求直線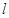 的方程;
的方程;
(3)設M,P是圓O上任意兩點,點M關于x軸的對稱點為N,若直線MP、NP分別交于x軸于點(m,0)和(n,0),問mn是否為定值?若是,請求出該定值;若不是,請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com