
等比數列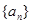 的前
的前 項和
項和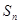 ,已知
,已知 ,
,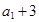 ,
,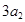 ,
,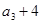 成等差數列.
成等差數列.
(1)求數列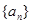 的公比
的公比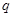 和通項
和通項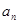 ;
;
(2)若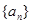 是遞增數列,令
是遞增數列,令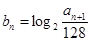 ,求
,求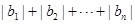 .
.
 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:高中數學 來源: 題型:解答題
已知數列{an}和{bn}滿足:a1=λ,an+1=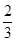 an+n-4,bn=(-1)n(an-3n+21),其中λ為實數,n為正整數.
an+n-4,bn=(-1)n(an-3n+21),其中λ為實數,n為正整數.
(1)對任意實數λ,證明:數列{an}不是等比數列;
(2)試判斷數列{bn}是否為等比數列,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
數列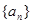 的首項為
的首項為 (
(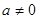 ),前
),前 項和為
項和為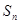 ,且
,且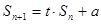 (
(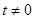 ).設
).設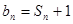 ,
, (
(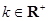 ).
).
(1)求數列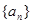 的通項公式;
的通項公式;
(2)當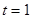 時,若對任意
時,若對任意 ,
,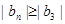 恒成立,求
恒成立,求 的取值范圍;
的取值范圍;
(3)當 時,試求三個正數
時,試求三個正數 ,
, ,
, 的一組值,使得
的一組值,使得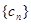 為等比數列,且
為等比數列,且 ,
, ,
, 成等差數列.
成等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知等比數列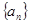 的公比為
的公比為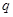 ,
,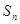 是
是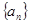 的前
的前 項和.
項和.
(1)若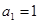 ,
,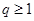 ,求
,求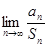 的值;
的值;
(2)若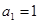 ,
,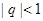 ,
,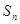 有無最值?并說明理由;
有無最值?并說明理由;
(3)設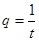 ,若首項
,若首項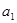 和
和 都是正整數,
都是正整數, 滿足不等式:
滿足不等式: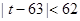 ,且對于任意正整數
,且對于任意正整數 有
有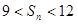 成立,問:這樣的數列
成立,問:這樣的數列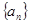 有幾個?
有幾個?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
大學生自主創業已成為當代潮流.某大學大三學生夏某今年一月初向銀行貸款兩萬元作開店資金,全部用作批發某種商品.銀行貸款的年利率為6%,約定一年后一次還清貸款.已知夏某每月月底獲得的利潤是該月月初投人資金的15%,每月月底需要交納個人所得稅為該月所獲利潤的20%,當月房租等其他開支1500元,余款作為資金全部投入批發該商品再經營,如此繼續,假定每月月底該商品能全部賣出.
(1)設夏某第n個月月底余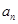 元,第n+l個月月底余
元,第n+l個月月底余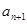 元,寫出a1的值并建立
元,寫出a1的值并建立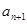 與
與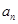 的遞推關系;
的遞推關系;
(2)預計年底夏某還清銀行貸款后的純收入.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
數列{an}是公比為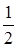 的等比數列,且1-a2是a1與1+a3的等比中項,前n項和為Sn;數列{bn}是等差數列,b1=8,其前n項和Tn滿足Tn=n
的等比數列,且1-a2是a1與1+a3的等比中項,前n項和為Sn;數列{bn}是等差數列,b1=8,其前n項和Tn滿足Tn=n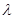 ·bn+1(
·bn+1(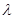 為常數,且
為常數,且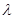 ≠1).
≠1).
(I)求數列{an}的通項公式及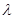 的值;
的值;
(Ⅱ)比較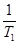 +
+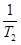 +
+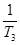 + +
+ +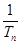 與
與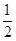 Sn的大小.
Sn的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com