
設各項均為正數的等比數列{an}中,a1+a3=10,a3+a5=40. 數列{bn}中,前n項和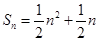
(1)求數列{an}與{bn}的通項公式;
(2)若c1=1,cn+1=cn+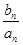 ,求數列
,求數列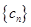 的通項公式
的通項公式
(3)是否存在正整數k,使得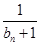 +
+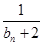 +…+
+…+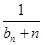 >
>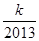 對任意正整數n均成立?若存在,求出k的最大值,若不存在,說明理由.
對任意正整數n均成立?若存在,求出k的最大值,若不存在,說明理由.
(1)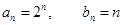 ) (2)
) (2) 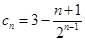 (3)
(3)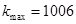
解析試題分析:(1)解:設數列{an}的公比為q(q>0),由a1+a3=10,a3+a5=40,則a1+a1q2=10①,a1q2+a1q4=40②∵a1≠0,②÷①得:q2=±2,又q>0,∴q=2.把q=2代入①得,a1=2.∴an=a1qn-1=2×2n-1=2n根據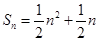 ,那么對于n=1,
,那么對于n=1,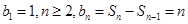 ,綜上可知
,綜上可知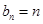
(2)那么可知c1=1,cn+1=cn+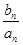 = cn+
= cn+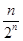 ,利用累加法可知
,利用累加法可知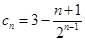
(3)假設存在正整數K,使得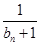 +
+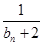 +…+
+…+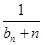 >
>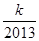 對任意正整數n均成立,則只要求解
對任意正整數n均成立,則只要求解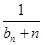 的前n項和即可通過放縮法得到k的取值范圍,即
的前n項和即可通過放縮法得到k的取值范圍,即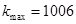 。
。
考點:等比數列的通項公式
點評:本題考查了等比數列的通項公式,考查了數列的遞推式,訓練了利用錯位相減法求數列的前n項和,屬中檔題.


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com