中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

用三段論推理命題：“任何實(shí)數(shù)的平方大于0，因?yàn)閍是實(shí)數(shù)，所以a2>0”，你認(rèn)為這個(gè)推理(   )

A．大前題錯(cuò)誤B．小前題錯(cuò)誤C．推理形式錯(cuò)誤 D．是正確的

A

解析試題分析：∵任何實(shí)數(shù)的平方大于0，因?yàn)閍是實(shí)數(shù)，所以a2＞0，
大前提：任何實(shí)數(shù)的平方大于0是不正確的，
故選A．
考點(diǎn)：演繹推理的基本方法．

練習(xí)冊(cè)系列答案
相關(guān)習(xí)題

科目：高中數(shù)學(xué) 來(lái)源： 題型：單選題

圖1，2，3，4分別包含1，5，13和25個(gè)互不重疊的單位正方形，按同樣的方式構(gòu)造圖形，則第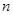個(gè)圖包含______個(gè)互不重疊的單位正方形。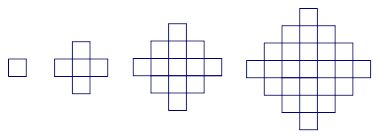

圖1      圖2         圖3              圖4

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：單選題

法國(guó)數(shù)學(xué)家費(fèi)馬觀察到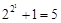，，，都是質(zhì)數(shù)，于是他提出猜想：任何形如N*）的數(shù)都是質(zhì)數(shù)，這就是著名的費(fèi)馬猜想. 半個(gè)世紀(jì)之后，善于發(fā)現(xiàn)的歐拉發(fā)現(xiàn)第5個(gè)費(fèi)馬數(shù)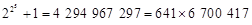不是質(zhì)數(shù)，從而推翻了費(fèi)馬猜想，這一案例說(shuō)明( )

A．歸納推理，結(jié)果一定不正確B．歸納推理，結(jié)果不一定正確
C．類比推理，結(jié)果一定不正確D．類比推理，結(jié)果不一定正確

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：單選題

用反證法證明命題：“若整系數(shù)一元二次方程有有理根，那么中至少有一個(gè)是偶數(shù)時(shí)，下列假設(shè)中正確的是

A．假設(shè)都是偶數(shù)
B．假設(shè)都不是偶數(shù)
C．假設(shè)至多有一個(gè)是偶數(shù)
D．假設(shè)至多有兩個(gè)是偶數(shù)

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：單選題

用反證法證明“自然數(shù)a，b，c中恰有一個(gè)偶數(shù)”時(shí)，下列假設(shè)正確的是   （   ）

A．假設(shè)a，b，c都是奇數(shù)或至少有兩個(gè)偶數(shù)
B．假設(shè)a，b，c都是偶數(shù)
C．假設(shè)a，b，c至少有兩個(gè)偶數(shù)
D．假設(shè)a， b，c都是奇數(shù)

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：填空題

下面是一個(gè)算法．如果輸出的y的值是20，則輸入的x的值是          .

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：單選題

用數(shù)學(xué)歸納法證明1＋2＋3＋…＋n2＝，則當(dāng)n＝k＋1時(shí)左端應(yīng)在n＝k的基礎(chǔ)上加上(　　)

A．k2＋1
B．(k＋1)2
C．
D．(k2＋1)＋(k2＋2)＋…＋(k＋1)2

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：單選題

若P＝＋，Q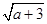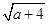＝＋ (a≥0)，則P，Q的大小關(guān)系(　　)

A．P>QB．P＝Q
C．P<QD．由a取值決定

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：單選題

給出下面類比推理命題(其中Q為有理數(shù)集，R為實(shí)數(shù)集，C為復(fù)數(shù)集)：
①“若a，b∈R，則a－b＝0⇒a＝b”，類比推出“若a，b∈C，則a－b＝0⇒a＝b”；
②“若a，b，c，d∈R，則復(fù)數(shù)a＋bi＝c＋di⇒a＝c，b＝d”，類比推出，“若a，b，c，d∈Q，則a＋b＝c＋d⇒a＝c，b＝d”；
③“若a，b∈R，則a－b>0⇒a>b”，類比推出“若a，b∈C，則a－b>0⇒a>b”；
④“若x∈R，則|x|<1⇒－1<x<1”，類比推出“若z∈C，則|z|<1⇒－1<z<1”．
其中類比正確的為(　　)

A．①② B．①④ C．①②③ D．②③④ 

查看答案和解析>>

同步練習(xí)冊(cè)答案