
 平面
平面 ,四邊形
,四邊形 是矩形,
是矩形, ,
, ,點
,點 ,
, 分別是
分別是 ,
, 的中點.
的中點.
 的體積;
的體積;  平面
平面 ;
; 為線段
為線段 中點,求證:
中點,求證: ∥平面
∥平面 .
.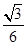 ;(Ⅱ)詳見解析;(Ⅲ)詳見解析
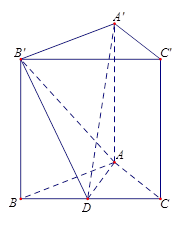
;(Ⅱ)詳見解析;(Ⅲ)詳見解析 平面
平面 ,所以
,所以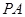 為三棱錐
為三棱錐 的高。因為
的高。因為 是矩形,所以可求底面
是矩形,所以可求底面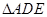 的面積,根據(jù)錐體體積公式
的面積,根據(jù)錐體體積公式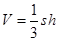 可求此三棱錐的體積。(Ⅱ)根據(jù)
可求此三棱錐的體積。(Ⅱ)根據(jù) 平面
平面 ,四邊形
,四邊形 是矩形,可證得
是矩形,可證得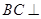 平面
平面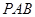 ,從而可得
,從而可得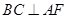 ,再根據(jù)等腰三角形中線即為高線可得
,再根據(jù)等腰三角形中線即為高線可得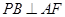 ,根據(jù)線面垂直的判定定理可得
,根據(jù)線面垂直的判定定理可得 平面
平面 。(Ⅲ)連結(jié)
。(Ⅲ)連結(jié)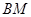 交
交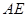 于
于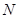 ,可證得
,可證得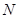 為
為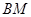 中點,由中位線可證得
中點,由中位線可證得 ∥
∥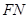 ,再由線面平行的判定定理可證得
,再由線面平行的判定定理可證得 ∥平面
∥平面 。
。 平面
平面 ,
,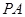 為三棱錐
為三棱錐 的高. 2分
的高. 2分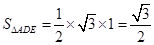 ,
,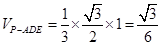 . 4分
. 4分 平面
平面 ,
,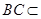 平面
平面 ,所以
,所以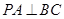 ,
, 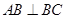 ,
,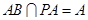 所以
所以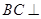 平面
平面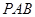
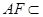 平面
平面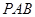 , 所以
, 所以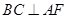 . 6分
. 6分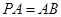 ,點
,點 是
是 的中點,所以
的中點,所以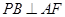 ,又因為
,又因為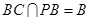 ,
, 平面
平面 . 8分
. 8分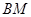 交
交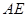 于
于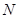 ,連結(jié)
,連結(jié) ,
,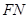 .
.
 是矩形,所以
是矩形,所以 ,且
,且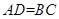 ,
, ,
, 分別為
分別為 ,
, 的中點, 所以四邊形
的中點, 所以四邊形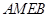 是平行四邊形,
是平行四邊形,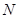 為
為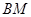 的中點,又因為
的中點,又因為 是
是 的中點,
的中點, ∥
∥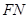 , 13分
, 13分 平面
平面 ,
,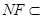 平面
平面 ,
, ∥平面
∥平面 . 14分
. 14分

科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
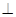 B'D;
B'D;查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
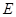 是以
是以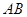 為直徑的半圓上異于點
為直徑的半圓上異于點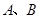 的點,矩形
的點,矩形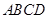 所在的平面垂直于該半圓所在平面,且
所在的平面垂直于該半圓所在平面,且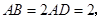
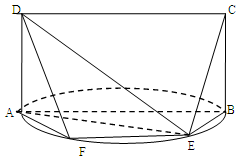
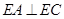 ;
;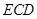 與半圓弧的另一個交點為
與半圓弧的另一個交點為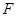 ,
,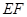 //
//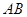 ;
;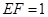 ,求三棱錐E-ADF的體積.
,求三棱錐E-ADF的體積.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
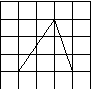
A. | B.3 | C.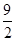 | D.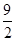  |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
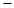 ABC中,E,F分別是AC,PC的中點,若EF
ABC中,E,F分別是AC,PC的中點,若EF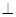 BF,AB=2,則三棱錐P
BF,AB=2,則三棱錐P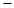 ABC的外接球的表面積為_________.
ABC的外接球的表面積為_________.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
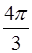 ,則圓錐的體積是________
,則圓錐的體積是________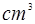 .
.查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com