
(本小題13分)已知數列{an}的前n項和Sn = 2an – 3×2n + 4 (n∈N*)
(1)求數列{an}的通項公式an;(2)設Tn為數列{Sn – 4}的前n項和,試比較Tn與14的大小.
(Ⅰ) an = (![]() n –
n – ![]() )2n,n∈N* (Ⅱ) 當n = 1,2時Tn<14.當n≥3時, Tn>14.
)2n,n∈N* (Ⅱ) 當n = 1,2時Tn<14.當n≥3時, Tn>14.
(1)由a1 = S1 = 2a1 – 3×2 + 4得a1 = 2,……1分
由已知,得Sn + 1 – Sn = 2 (an + 1 – an) – (2n + 1 – 2n) 即an + 1 = 2an + 3×2n 兩邊同除以2n + 1得![]() 即
即![]() ∴數列{
∴數列{![]() }是以
}是以![]() = 1為首項,
= 1為首項,![]() 為公差的等差數列.
為公差的等差數列.
∴![]() = 1 + (n – 1) ×
= 1 + (n – 1) ×![]() 即an = (
即an = (![]() n –
n – ![]() )2n,n∈N*.……6分
)2n,n∈N*.……6分
(2)∵Sn – 4 = 2an – 3×2n = (3n – 4)·2n.∴Tn = –1×2 + 2·22 + 5·23 + …+ (3n – 4)·2n①2Tn = –1×22 + 2×23 + … + (3n – 7)·2n + (3n – 4)·2n + 1 ②
① – ②得 –Tn = –2 + 3(22 + 23 + …+2n) – (3n – 4)·2n + 1
= –2 + 3×![]() – (3n – 4)·2n + 1 = –14 + (14 – 6n)·2n ……10分
– (3n – 4)·2n + 1 = –14 + (14 – 6n)·2n ……10分
∴Tn = 14 – (14 – 6n)·2n.∵當n = 1,2時,14 – 6n>0
∴Tn<14.當n≥3時,14 – 6n>0 ∴Tn>14.……13分


科目:高中數學 來源:2011-2012學年北京市示范校高三12月綜合練習(一)文科數學 題型:解答題
(本小題13分)
已知等比數列 滿足
滿足 ,且
,且 是
是 ,
, 的等差中項.
的等差中項.
(Ⅰ)求數列 的通項公式;
的通項公式;
(Ⅱ)若 ,
, ,求使
,求使
 成立的正整數
成立的正整數 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源:2011年福建省高一上學期期末考試數學理卷 題型:解答題
(本小題13分)
已知直線 過直線
過直線 和
和 的交點;
的交點;
(Ⅰ)若直線 與直線
與直線 垂直,求直線
垂直,求直線 的方程.
的方程.
(Ⅱ)若原點 到直線
到直線 的距離為1.求直線
的距離為1.求直線 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年江西省協作體高三第二次聯考數學理卷 題型:解答題
(本小題13分)
已知拋物線方程為 ,過
,過 作直線
作直線 .
.
①若 與
與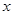 軸不垂直,交拋物線于A、B兩點,是否存在
軸不垂直,交拋物線于A、B兩點,是否存在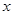 軸上一定點
軸上一定點 ,使得
,使得 ?若存在,求出m的值;若不存在,請說明理由?
?若存在,求出m的值;若不存在,請說明理由?
②若 與
與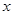 軸垂直,拋物線的任一切線與
軸垂直,拋物線的任一切線與 軸和
軸和 分別交于M、N兩點,則自點M到以QN為直徑的圓的切線長
分別交于M、N兩點,則自點M到以QN為直徑的圓的切線長 為定值,試證之;
為定值,試證之;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com