
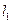 、
、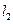 、
、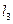 是同一平面內三條不重合自上而下的平行直線.
是同一平面內三條不重合自上而下的平行直線.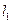 與
與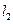 間的距離是1,
間的距離是1,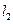 與
與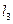 間的距離也是1,可以把一個正三角形
間的距離也是1,可以把一個正三角形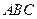 的三頂點分別放在
的三頂點分別放在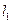 ,
,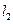 ,
,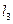 上,求這個正三角形
上,求這個正三角形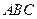 的邊長;
的邊長;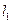 與
與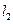 間的距離是1,
間的距離是1,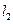 與
與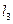 間的距離是2,能否把一個正三角形
間的距離是2,能否把一個正三角形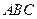 的三頂點分別放在
的三頂點分別放在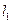 ,
,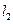 ,
,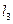 上,如果能放,求
上,如果能放,求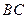 和
和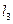 夾角的正切值并求該正三角形邊長;如果不能,說明為什么?
夾角的正切值并求該正三角形邊長;如果不能,說明為什么?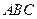 的三頂點分別在
的三頂點分別在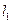 ,
,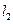 ,
,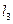 上,設
上,設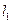 與
與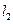 的距離為
的距離為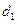 ,
,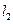 與
與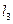 的距離為
的距離為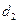 ,求
,求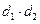 的范圍?
的范圍?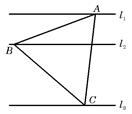
 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源:不詳 題型:解答題
 求證:m≥5;
求證:m≥5;查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| πx |
| 3 |
| πx |
| 5 |
| πx |
| 3 |
| πx |
| 5 |
| A.30π | B.15π | C.30 | D.15 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com