
去年2月29日,我國發布了新修訂的《環境空氣質量標準》指出空氣質量指數在 為優秀,各類人群可正常活動.惠州市環保局對我市2014年進行為期一年的空氣質量監測,得到每天的空氣質量指數,從中隨機抽取50個作為樣本進行分析報告,樣本數據分組區間為
為優秀,各類人群可正常活動.惠州市環保局對我市2014年進行為期一年的空氣質量監測,得到每天的空氣質量指數,從中隨機抽取50個作為樣本進行分析報告,樣本數據分組區間為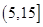 ,
,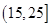 ,
,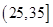 ,
,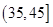 ,由此得到樣本的空氣質量指數頻率分布直方圖,如圖.
,由此得到樣本的空氣質量指數頻率分布直方圖,如圖.
(1) 求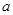 的值;
的值;
(2) 根據樣本數據,試估計這一年度的空氣質量指數的平均值;(注:設樣本數據第 組的頻率為
組的頻率為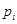 ,第
,第 組區間的中點值為
組區間的中點值為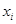
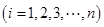 ,則樣本數據的平均值為
,則樣本數據的平均值為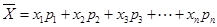 .)
.)
(3) 如果空氣質量指數不超過 ,就認定空氣質量為“特優等級”,則從這一年的監測數據中隨機抽取
,就認定空氣質量為“特優等級”,則從這一年的監測數據中隨機抽取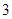 天的數值,其中達到“特優等級”的天數為
天的數值,其中達到“特優等級”的天數為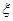 ,求
,求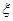 的分布列和數學期望.
的分布列和數學期望.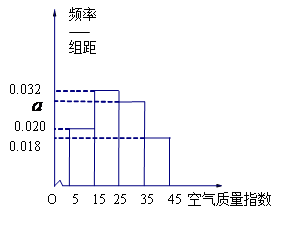
(1)0.03;(2)24.6;(3)分布列詳見解析,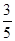 .
.
解析試題分析:本題主要考查頻率分布直方圖、由樣本估計總體求平均值、二項分布、離散型隨機變量的分布列和數學期望等基礎知識,考查學生的分析問題解決問題的能力、計算能力、轉化能力.第一問,利用頻率分布直方圖中長方形的高=頻率/組距,而所有頻率之和為1,來計算a的值;第二問,根據樣本數據,估計總體的平均值的計算公式為:頻率分布直方圖中,每一個長方形的中點×高×組距,得到的數據之和即為平均值;第三問,利用頻率分布直方圖先得到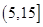 內的頻率,即“特優等級”的概率值,通過分析題意可知隨機變量
內的頻率,即“特優等級”的概率值,通過分析題意可知隨機變量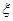 服從二項分布,利用
服從二項分布,利用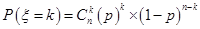 計算出每一種情況的概率,再利用
計算出每一種情況的概率,再利用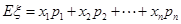 計算出數學期望
計算出數學期望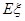 .
.
試題解析:(1) 由題意,得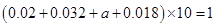 , 1分
, 1分
解得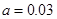 . 2分
. 2分
(2)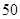 個樣本中空氣質量指數的平均值為
個樣本中空氣質量指數的平均值為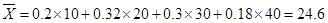 3分
3分
由樣本估計總體,可估計這一年度空氣質量指數的平均值約為 . 4分
. 4分
(3)利用樣本估計總體,該年度空氣質量指數在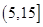 內為“特優等級”,
內為“特優等級”,
且指數達到“特優等級”的概率為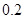 ,則
,則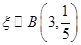 . 5分
. 5分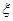 的取值為
的取值為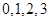 , 6分
, 6分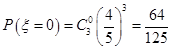 ,
,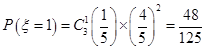 ,
,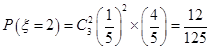 ,
,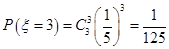 . 10分
. 10分
∴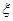 的分布列為:
的分布列為:
11分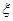

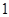
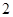
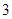
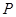
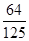
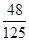
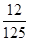
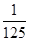
∴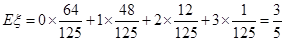 . 12分
. 12分
(或者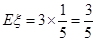 )
)
考點:頻率分布直方圖、由樣本估計總體求平均值、二項分布、離散型隨機變量的分布列和數學期望.


科目:高中數學 來源: 題型:解答題
從天氣網查詢到衡水歷史天氣統計 (2011-01-01到2014-03-01)資料如下: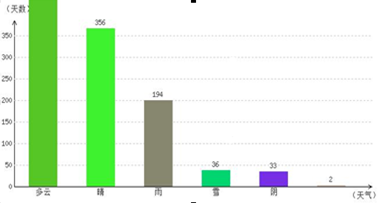
自2011-01-01到2014-03-01,衡水共出現:多云507天,晴356天,雨194天,雪36天,陰33天,其它2天,合計天數為:1128天。
本市朱先生在雨雪天的情況下,分別以 的概率乘公交或打出租的方式上班(每天一次,且交通方式僅選一種),每天交通費用相應為2元或40元;在非雨雪天的情況下,他以90%的概率騎自行車上班,每天交通費用0元;另外以10%的概率打出租上班,每天交通費用20元。(以頻率代替概率,保留兩位小數.參考數據:
的概率乘公交或打出租的方式上班(每天一次,且交通方式僅選一種),每天交通費用相應為2元或40元;在非雨雪天的情況下,他以90%的概率騎自行車上班,每天交通費用0元;另外以10%的概率打出租上班,每天交通費用20元。(以頻率代替概率,保留兩位小數.參考數據: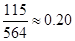 )
)
(1)求他某天打出租上班的概率;
(2)將他每天上班所需的費用記為 (單位:元),求
(單位:元),求 的分布列及數學期望。
的分布列及數學期望。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲有大小相同的兩張卡片,標有數字2、3;乙有大小相同的卡片四張,分別標有1、2、3、4.
(1)求乙隨機抽取的兩張卡片的數字之和為奇數的概率;
(2)甲、乙分別取出一張卡,比較數字,數字大者獲勝,求乙獲勝的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校從高一年級周末考試的學生中抽出6O名學生,其成績(均為整數)的頻率分布直方圖如圖所示:(1)依據頻率分布直方圖,估計這次考試的及格率(60分及以上為及格)和平均分;(2)已知在[90,100]段的學生的成績都不相同,且都在94分以上,現用簡單隨機抽樣方法,從95,96,97,98,99,100這6個數中任取2個數,求這2個數恰好是兩個學生的成績的概率.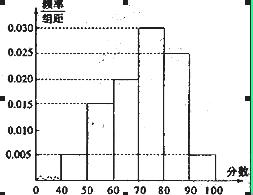
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某地區為了解高二學生作業量和玩電腦游戲的情況,對該地區內所有高二學生采用隨機抽樣的方法,得到一個容量為200的樣本.統計數據如下:
(1)已知該地區共有高二學生42500名,根據該樣本估計總體,其中喜歡電腦游戲并認為作業不多的人有多少名?
(2)在A,B,C,D,E,F六名學生中,僅有A,B兩名學生認為作業多.如果從這六名學生中隨機抽取兩名,求至少有一名學生認為作業多的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,某中學甲、乙兩班共有25名學生報名參加了一項 測試.這25位學生的考分編成的莖葉圖,其中有一個數據因電腦操作員不小心刪掉了(這里暫用x來表示),但他清楚地記得兩班學生成績的中位數相同.
(1)求這兩個班學生成績的中位數及x的值;
(2)如果將這些成績分為“優秀”(得分在175分以上,包括175分)和“過關”,若學校再從這兩個班獲得“優秀”成績的考生中選出3名代表學校參加比賽,求這3人中甲班至多有一人入選的概率.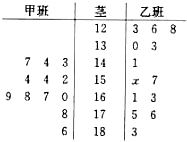
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知 、
、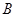 兩盒中都有紅球、白球,且球的形狀、大小都相同,盒子
兩盒中都有紅球、白球,且球的形狀、大小都相同,盒子 中有
中有 個紅球與
個紅球與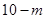 個白球,盒子
個白球,盒子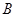 中有
中有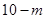 個紅球與
個紅球與 個白球(
個白球(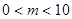 ).
).
(1)分別從 、
、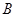 中各取一個球,
中各取一個球, 表示紅球的個數;
表示紅球的個數;
①請寫出隨機變量 的分布列,并證明
的分布列,并證明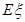 等于定值;
等于定值;
②當 為何值時,
為何值時,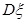 取到最小值,并求出最小值.
取到最小值,并求出最小值.
(2)在盒子 中不放回地摸取3個球,事件
中不放回地摸取3個球,事件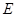 :在第一次取到紅球后,以后兩次都取到白球,事件
:在第一次取到紅球后,以后兩次都取到白球,事件 :在第一次取到白球后,以后兩次都取到紅球,若概率
:在第一次取到白球后,以后兩次都取到紅球,若概率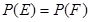 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工藝廠開發一種新工藝品,頭兩天試制中,該廠要求每位師傅每天制作10件,該廠質檢部每天從每位師傅制作的10件產品中隨機抽取4件進行檢查,若發現有次品,則當天該師傅的產品不能通過.已知李師傅第一天、第二天制作的工藝品中分別有2件、1件次品.
(1)求兩天中李師傅的產品全部通過檢查的概率;
(2)若廠內對師傅們制作的工藝品采用記分制,兩天都不通過檢查的得0分,兩天中只通過一天檢查的得1分,兩天都通過檢查的得2分,求李師傅在這兩天內得分的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com