
已知函數 .
.
(1)當 時,求曲線
時,求曲線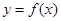 在點
在點 處的切線方程;
處的切線方程;
(2)當 ,且
,且 ,求函數
,求函數 的單調區(qū)間.
的單調區(qū)間.
(1) 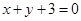 ;(2)當
;(2)當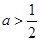 時,
時, 在
在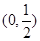 ,
,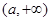 上單調遞增,在
上單調遞增,在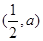 上單調遞減,當
上單調遞減,當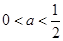 時,
時, 在
在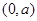 ,
,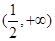 上單調遞增,在
上單調遞增,在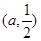 上單調遞減.
上單調遞減.
解析試題分析:本題綜合考查函數與導數及運用導數求單調區(qū)間和切線方程等數學知識和方法,考查函數思想、分類討論思想.第一問,先把 代入,得到
代入,得到 解析式,對它求導,將切點的橫坐標代入得到切線的斜率,將1代入到
解析式,對它求導,將切點的橫坐標代入得到切線的斜率,將1代入到 表達式中得到切點的縱坐標,最后通過點斜式方程直接寫出切線方程;第二問,先對
表達式中得到切點的縱坐標,最后通過點斜式方程直接寫出切線方程;第二問,先對 求導,令
求導,令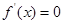 得到方程的2個根
得到方程的2個根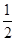 和
和 ,討論
,討論 和
和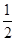 的大小,分情況令
的大小,分情況令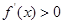 得函數的增區(qū)間,
得函數的增區(qū)間, 得函數的減區(qū)間.
得函數的減區(qū)間.
試題解析:(1)當 時,
時,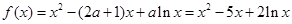 ,
,
∴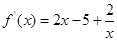 ,(2分)
,(2分)
∴ ,
,
又 ,(4分)
,(4分)
∴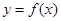 在點
在點 處的切線方程為
處的切線方程為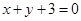 .(5分)
.(5分)
(2)  (
(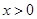 ),
),
令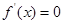 ,可得
,可得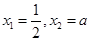 .(6分)
.(6分)
①當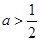 時,由
時,由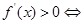
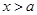 或
或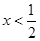 ,
, 在
在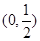 ,
,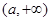 上單調遞增.
上單調遞增.
由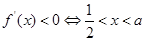 .
. 在
在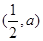 上單調遞減.(9分)
上單調遞減.(9分)
②當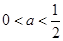 時,由
時,由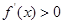 可得
可得 在
在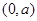 ,
,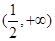 上單調遞增.
上單調遞增.
由 可得
可得 在
在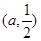 上單調遞減.(12分)
上單調遞減.(12分)
考點:1.利用導數求切線方程;2.利用導數求函數的單調區(qū)間.


國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com