
已知函數 ,函數
,函數 的導函數
的導函數 ,且
,且 ,其中
,其中 為自然對數的底數.
為自然對數的底數.
(1)求 的極值;
的極值;
(2)若 ,使得不等式
,使得不等式 成立,試求實數
成立,試求實數 的取值范圍;
的取值范圍;
(3)當 時,對于
時,對于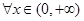 ,求證:
,求證: .
.
(1)當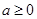 時,
時, 沒有極值;
沒有極值;
當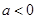 時,
時, 存在極大值,且當
存在極大值,且當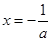 時,
時,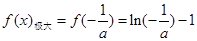 .
.
(2)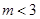 .
.
(3)見解析.
解析試題分析:(1) 首先確定函數 的定義域為
的定義域為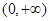 ,求導數
,求導數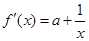
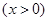 .為確定函數的極值,應討論
.為確定函數的極值,應討論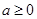 ,
,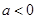 的不同情況.
的不同情況.
(2) 首先求出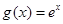 ,將問題轉化成
,將問題轉化成 ,使得
,使得 成立,
成立,
引入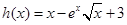 ,將問題可轉化為:
,將問題可轉化為:
利用導數求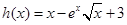 的最大值,得解.
的最大值,得解.
(3)當 時,
時,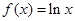 ,構造函數
,構造函數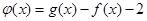 ,即
,即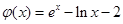 ,
,
應用導數研究函數的單調性、極值,得到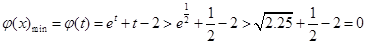 .
.
方法比較明確,分類討論、轉化與化歸思想的應用,是解決問題的關鍵.
試題解析:(1) 函數 的定義域為
的定義域為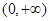 ,
,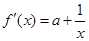
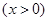 .
.
當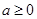 時,
時, ,
,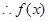 在
在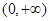 上為增函數,
上為增函數, 沒有極值; 1分
沒有極值; 1分
當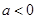 時,
時,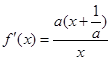 ,
,
若 時,
時, ;若
;若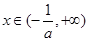 時,
時,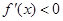
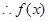 存在極大值,且當
存在極大值,且當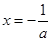 時,
時,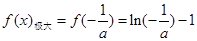
綜上可知:當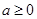 時,
時, 沒有極值;當
沒有極值;當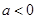 時,
時, 存在極大值,且當
存在極大值,且當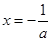 時,
時,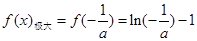 4分
4分
(2) 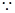 函數
函數 的導函數
的導函數 ,
,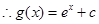
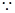
 ,
,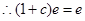
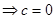 ,
,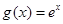 5分
5分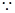
 ,使得不等式
,使得不等式 成立,
成立,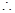
 ,使得
,使得 成立,
成立,
令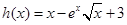 ,則問題可轉化為:
,則問題可轉化為:
對于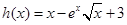 ,
,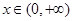 ,由于
,由于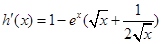 ,
,
當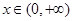 時,
時,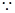
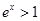 ,
, ,
,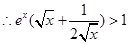 ,
,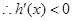 ,從而
,從而 在
在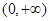 上為減函數,
上為減函數,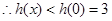
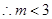 &nbs
&nbs


 應用題作業本系列答案
應用題作業本系列答案科目:高中數學 來源: 題型:解答題
已知函數f(x)=ax2-ln x,x∈(0,e],其中e是自然對數的底數,a∈R.
(1)當a=1時,求函數f(x)的單調區間與極值;
(2)是否存在實數a,使f(x)的最小值是3?若存在,求出a的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=ax3+3x2-6ax-11,g(x)=3x2+6x+12和直線m:y=kx+9,且f′(-1)=0.
(1)求a的值.
(2)是否存在k的值,使直線m既是曲線y=f(x)的切線,又是曲線y=g(x)的切線?如果存在,求出k的值;如果不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 ;
;
(1)若 >0,試判斷f(x)在定義域內的單調性;
>0,試判斷f(x)在定義域內的單調性;
(2)若f(x)在[1,e]上的最小值為 ,求
,求 的值;
的值;
(3)若f(x)<x2在(1, 上恒成立,求a的取值范圍.
上恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某村莊擬修建一個無蓋的圓柱形蓄水池(不計厚度).設該蓄水池的底面半徑為r米,高為h米,體積為V立方米.假設建造成本僅與表面積有關,側面的建造成本為100元/平方米,底面的建造成本為160元/平方米,該蓄水池的總建造成本為12 000π元(π為圓周率).
(1)將V表示成r的函數V(r),并求該函數的定義域;
(2)討論函數V(r)的單調性,并確定r和h為何值時該蓄水池的體積最大.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)= .
.
(1)確定y=f(x)在(0,+∞)上的單調性;
(2)若a>0,函數h(x)=xf(x)-x-ax2在(0,2)上有極值,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=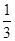 ax3-
ax3- x2+cx+d(a,c,d∈R)滿足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)滿足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
(1)求a,c,d的值;
(2)若h(x)=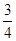 x2-bx+
x2-bx+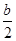 -
- ,解不等式f′(x)+h(x)<0.
,解不等式f′(x)+h(x)<0.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com