
設向量 .
.
⑴若 ,求
,求 的值;
的值;
⑵設函數 ,求
,求 的最大值.
的最大值.
(1)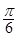 ;(2)
;(2) .
.
解析試題分析:(1)題中唯一已知條件是兩個向量的模相等,那么我們把這個條件化簡得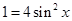 ,這樣正好解出
,這樣正好解出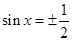 ,由三角函數值求角,還要確定角的范圍,本題中
,由三角函數值求角,還要確定角的范圍,本題中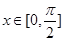 ,
,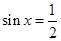 ,從而有
,從而有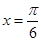 .
.
(2)同(1)把 化簡,變?yōu)槲覀兪煜さ暮瘮担?img src="http://thumb.zyjl.cn/pic5/tikupic/f6/a/tcrgf3.png" style="vertical-align:middle;" />,這是三角函數,一般要化為
化簡,變?yōu)槲覀兪煜さ暮瘮担?img src="http://thumb.zyjl.cn/pic5/tikupic/f6/a/tcrgf3.png" style="vertical-align:middle;" />,這是三角函數,一般要化為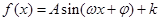 形式,然后利用正弦函數的性質解決問題,
形式,然后利用正弦函數的性質解決問題,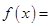
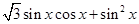

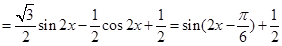 ,
,
因此 最大值為
最大值為 .
.
試題解析:(1)∵ ,∴
,∴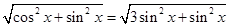 ,
,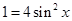 ,∵
,∵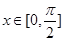 ,∴
,∴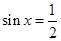 ,
,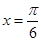 . 7分
. 7分
(2)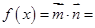
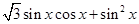

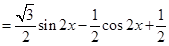
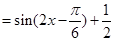
∵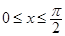 ∴
∴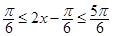
∴ 最大值為
最大值為 . 14分
. 14分
考點:(1)已知三角函數值,求角;(2)三角函數的最大值.


 高中必刷題系列答案
高中必刷題系列答案科目:高中數學 來源: 題型:解答題
已知向量 ,
, ,函數
,函數 .將函數
.將函數 的圖象上各點的縱坐標保持不變,橫坐標先縮短到原來的
的圖象上各點的縱坐標保持不變,橫坐標先縮短到原來的 ,把所得到的圖象再向左平移
,把所得到的圖象再向左平移 個單位,得到函數
個單位,得到函數 的圖象.
的圖象.
(1)求函數 的單調遞增區(qū)間;
的單調遞增區(qū)間;
(2)若 ,求
,求 的值.
的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com