分析:(1)取AB中點F,連接EF、CF.根據(jù)線面垂直的性質證出EF⊥AB,結合正△ABC中,中線CF⊥AB,所以AB⊥平面CEF,從而可得AB⊥CE;
(2)以F點為坐標原點,又FB,F(xiàn)C,F(xiàn)E為x,y,z軸正方向建立空間坐標系,分別求出異面直線AD與BC的方向向量,代入向量夾角公式,可得答案.
解答: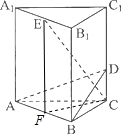
證明:(1)取AB中點F,連接EF、CF
∵三棱柱ABC-A
1B
1C
1是正三棱柱,
∴側面AA
1B
1B是矩形
∵E、F分別是A
1B
1、AB的中點,∴EF∥AA
1,
∵AA
1⊥平面ABC,AB⊆平面ABC,∴AA
1⊥AB,可得EF⊥AB,
∵正△ABC中,CF是中線,∴CF⊥AB
∵EF∩CF=F,∴AB⊥平面CEF
∵CE⊆平面CEF,∴AB⊥CE;
(2)以F點為坐標原點,又FB,F(xiàn)C,F(xiàn)E為x,y,z軸正方向建立空間坐標系,
∵底面邊長和側棱長都是3,D是側棱CC
1上一點且C
1D=2DC,
∴A(
-,0,0),B(
,0,0),C(0,
,0),D(0,
,1)
∴
=(
,
,1),
=(
-,
,0),
設直線AD與BC所成角為θ
則cosθ=
=
=
即直線AD與BC所成角的余弦值為
點評:本題給出所有棱長都相等的正三棱柱,證明線線垂直及異面直線的夾角,(1)的關鍵是熟練掌握空間線線垂直與線面垂直之間的相互轉化,(2)的關鍵是建立空間坐標系,將異面直線的夾角轉化為向量的夾角.

 如圖所示,在正三棱柱ABC-A1B1C1中,底面邊長和側棱長都是3,D是側棱CC1上一點且C1D=2DC,E是A1B1的中點.
如圖所示,在正三棱柱ABC-A1B1C1中,底面邊長和側棱長都是3,D是側棱CC1上一點且C1D=2DC,E是A1B1的中點. 證明:(1)取AB中點F,連接EF、CF
證明:(1)取AB中點F,連接EF、CF

 智慧小復習系列答案
智慧小復習系列答案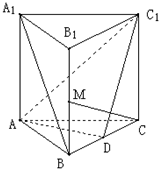 如圖所示,在正三棱柱ABC-A1B1C1中,底面邊長是2,D是棱BC的中點,點M 是棱BB1的中點,又CM⊥AC1,
如圖所示,在正三棱柱ABC-A1B1C1中,底面邊長是2,D是棱BC的中點,點M 是棱BB1的中點,又CM⊥AC1,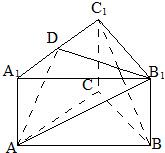 如圖所示,在正三棱柱ABC-A1B1C1中,底面邊長為a,側棱長為
如圖所示,在正三棱柱ABC-A1B1C1中,底面邊長為a,側棱長為 如圖所示,在正三棱柱ABC-A1B1C1中,底面邊長是2,D是棱BC的中點,點M在棱BB1上,且BM=
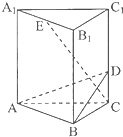
如圖所示,在正三棱柱ABC-A1B1C1中,底面邊長是2,D是棱BC的中點,點M在棱BB1上,且BM= (2012•日照一模)如圖所示,在正三棱柱ABC-A1B1C1中,底面邊長和側棱長都是2,D是側棱CC1上任意一點,E是A1B1的中點.
(2012•日照一模)如圖所示,在正三棱柱ABC-A1B1C1中,底面邊長和側棱長都是2,D是側棱CC1上任意一點,E是A1B1的中點.