

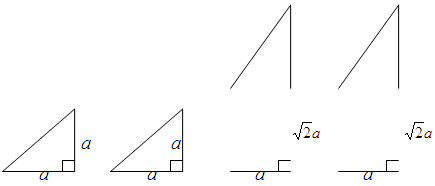
 面ABCD,E為AB中點,求證:面
面ABCD,E為AB中點,求證:面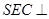 面
面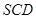
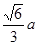

 底面ABCD………………3分
底面ABCD………………3分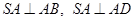 ,且AB、AD是面ABCD內兩條相交直線
,且AB、AD是面ABCD內兩條相交直線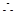 SA
SA 底面ABCD……………………5分
底面ABCD……………………5分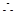 AF//EG
AF//EG 面ABCD得SA
面ABCD得SA CD,
CD, CD,
CD,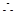 CD
CD 面SAD,
面SAD,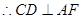
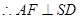
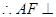 面SCD,即EG
面SCD,即EG 面SCD,
面SCD, 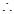 面
面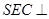 面
面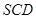 …………10分
…………10分 SC于H,
SC于H, 面SCD,
面SCD,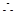 DH
DH 面SEC,
面SEC,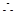 DH之長即為點D到面SEC的距離,12分
DH之長即為點D到面SEC的距離,12分 SCD中,
SCD中,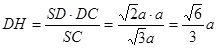
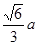 …………14分
…………14分

 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:高中數學 來源:不詳 題型:解答題
 a(0<
a(0< ≦1).
≦1). 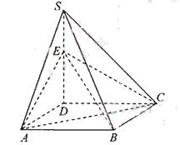

 (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE: 的值。
的值。查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
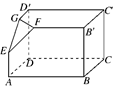
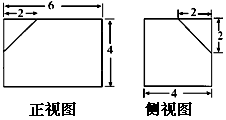
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com