(本小題滿分9分) 如圖,四棱錐S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,點E是SD上的點,且DE=

a(0<

≦1).
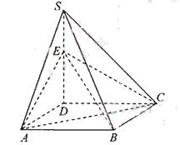
(Ⅰ)求證:對任意的

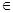
(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小為60
0C,求

的值。
(Ⅰ)見解析;(II)
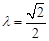
。
運用三垂線定理證明線線垂直,第二問是告訴二面角求參數(shù)的值,這是二面角的逆向問題,仍然要作出二面角,求二面角才能解出參數(shù)。這題除了用傳統(tǒng)的證法與求角的方法外,也可以應(yīng)用空間向量來解決。
解:(Ⅰ)證發(fā)1:連接BD,由底面是正方形可得AC

BD。
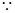
SD

平面ABCD,
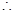
BD是BE在平面ABCD上的射影,
由三垂線定理得AC

BE.
(II)解法1:
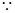
SD

平面ABCD,CD
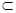
平面ABCD,
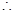
SD

CD.
又底面ABCD是正方形,
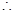
CD

AD,又SD
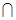
AD=D,
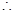
CD

平面SAD。
過點D在平面SAD內(nèi)做DF

AE于F,連接CF,則CF

AE,
故
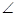
CFD是二面角C-AE-D 的平面角,即
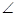
CFD=60°
在Rt△ADE中,
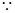
AD=
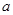
, DE=
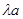
, AE=
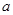
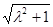
。
于是,DF=
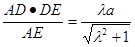
在Rt△CDF中,由

cot60°=
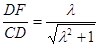
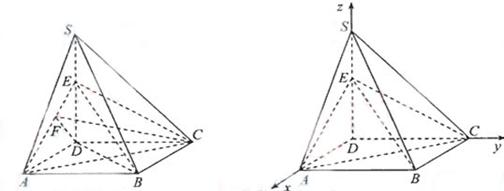
得
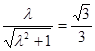
, 即
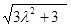
=3

解得
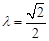
。
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,

矩形ABCD所在的平面,M,N分別為AB,PC的中點。求證:

平面


查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
下面的一組圖形為某一四棱錐S-ABCD的底面與側(cè)面。

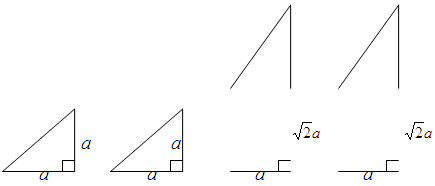
(1)請畫出四棱錐S-ABCD的示意圖,是否存在一條側(cè)棱垂直于底面?如果存在,請給出證明;如果不存在,請說明理由;
(2)若SA

面ABCD,E為AB中點,求證:面
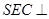
面
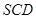
(3)求點D到面SEC的距離。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(滿分12分)設(shè)底面邊長為
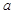
的正四棱柱
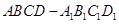
中,
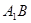
與平面
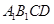
所成角為
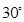
;點

是棱
上一點.
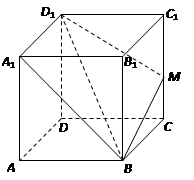
(1)求證:正四棱柱
是正方體;
(2)若點

在棱
上滑動,求點
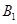
到平面
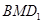
距離的最大值;
(3)在(2)的條件下,求二面角
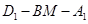
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
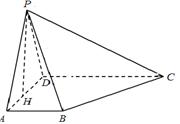
(本小題滿分14分)如圖所示,在四棱錐
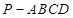
中,
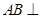
平面
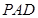
,
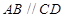
,
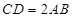
,
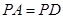
,
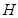
是
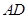
的中點.
(1)證明:
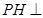
平面

;
(2)若
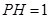
,
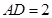
,
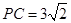
,求二面角

的正切值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(12分)已知三棱錐
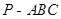
各側(cè)棱長均為
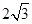
,三個頂角均為
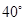
,M,N分別為PA,PC上的點,求
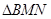
周長的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
長方體的一個頂點上三條棱的邊長分別為3、4、5,且它的八個頂點都在同一球
面上,這個球的表面積是( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
.點
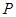
在正方體
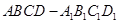
的面對角線
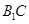
上運動,
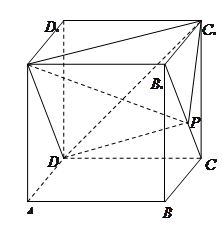
則下列四個命題中:(1)
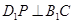
;
(2)
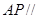
平面
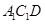
;
(3)三棱錐
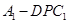
的體積隨點
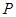
的運動而變化。
其中真命題的個數(shù)是( )
A.1 B.2 C.3 D.0
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
在棱長為
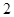
的正方體
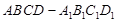
中,點
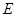
,
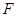
分別是棱
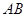
,
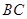
的中點,則點
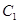
到平面
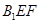
的距離是( ).
查看答案和解析>>

 a(0<
a(0< ≦1).
≦1). 

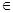 (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE: 的值。
的值。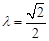 。
。 BD。
BD。 SD
SD 平面ABCD,
平面ABCD,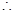 BD是BE在平面ABCD上的射影,
BD是BE在平面ABCD上的射影, BE.
BE.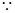 SD
SD 平面ABCD,CD
平面ABCD,CD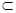 平面ABCD,
平面ABCD,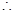 SD
SD CD.
CD. 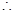 CD
CD AD,又SD
AD,又SD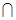 AD=D,
AD=D,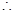 CD
CD 平面SAD。
平面SAD。 AE于F,連接CF,則CF
AE于F,連接CF,則CF AE,
AE, 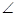 CFD是二面角C-AE-D 的平面角,即
CFD是二面角C-AE-D 的平面角,即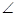 CFD=60°
CFD=60° 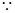 AD=
AD=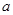 , DE=
, DE= 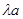 , AE=
, AE=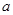
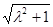 。
。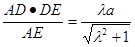
 cot60°=
cot60°=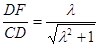

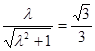 , 即
, 即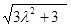 =3
=3 解得
解得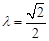 。
。


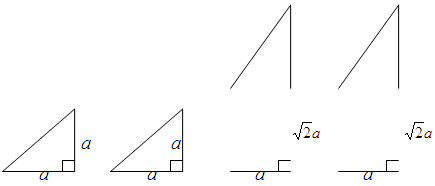
 面ABCD,E為AB中點,求證:面
面ABCD,E為AB中點,求證:面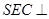 面
面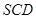
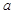 的正四棱柱
的正四棱柱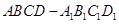 中,
中,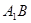 與平面
與平面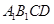 所成角為
所成角為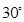 ;點
;點 是棱
是棱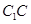 上一點.
上一點.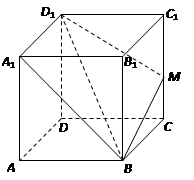
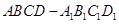 是正方體;
是正方體; 在棱
在棱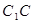 上滑動,求點
上滑動,求點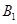 到平面
到平面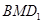 距離的最大值;
距離的最大值;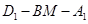 的大小.
的大小.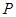 在正方體
在正方體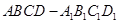 的面對角線
的面對角線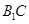 上運動,
上運動,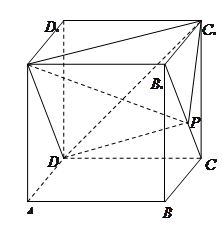
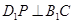 ;
;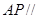 平面
平面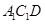 ;
;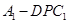 的體積隨點
的體積隨點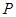 的運動而變化。
的運動而變化。