
|
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |


科目:高中數學 來源: 題型:
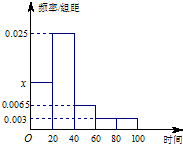 (2012•海淀區一模)某學校隨機抽取部分新生調查其上學所需時間(單位:分鐘),并將所得數據繪制成頻率分布直方圖(如圖),其中,上學所需時間的范圍是[0,100],樣本數據分組為[0,20),[20,40),[40,60),[60,80),[80,100].
(2012•海淀區一模)某學校隨機抽取部分新生調查其上學所需時間(單位:分鐘),并將所得數據繪制成頻率分布直方圖(如圖),其中,上學所需時間的范圍是[0,100],樣本數據分組為[0,20),[20,40),[40,60),[60,80),[80,100].查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com