
(09年濟寧質檢一理)(12分)
已知函數![]() .
.
(Ⅰ)當![]() 時,
時,![]() 使不等式
使不等式![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)若在區間![]() 上,函數
上,函數![]() 的圖象恒在直線
的圖象恒在直線![]() 的下方,求實數
的下方,求實數![]() 的取值范圍.
的取值范圍.
解析:(Ⅰ)當![]() 時
時![]() ,
,![]()
由![]() ,
,![]() 得函數
得函數![]() 在區間
在區間![]() 為增函數,
為增函數,
則當![]() 時
時![]() 。
。
故要使![]() 使不等式
使不等式![]() 成立,只需
成立,只需![]() 即可。
即可。
(Ⅱ)在區間![]() 上,函數
上,函數![]() 的圖象恒在直線
的圖象恒在直線![]() 的下方等價于
的下方等價于
對![]() ,
,![]()
![]() ,即
,即![]() 恒成立。
恒成立。
設![]() ,
,
則![]() .
.
當![]() 時,
時,![]() .
.
(1)若![]() ,即
,即![]() ,
,![]() ,函數
,函數![]() 在區間
在區間![]() 為減函數,
為減函數,
則當![]() 時
時![]() ,
,
只需![]() ,即當
,即當![]() 時
時![]() 恒成立.
恒成立.
(2)若![]() ,即
,即![]() 時,令
時,令![]() 得
得![]()
函數![]() 在區間
在區間![]() 為減函數,
為減函數,![]() 為增函數,
為增函數,
則![]() ,不合題意.
,不合題意.
(3)若![]() ,即當
,即當![]() 時
時![]() ,函數
,函數![]() 在區間
在區間![]() 為增函數,
為增函數,
則![]() ,不合題意.
,不合題意.
綜上可知當![]() 時
時![]() 恒成立,
恒成立,
即當![]() 時,在區間
時,在區間![]() 上函數
上函數![]() 的圖象恒在直線
的圖象恒在直線![]() 的下方。
的下方。
另解:對![]() ,
,![]()
![]() 恒成立,
恒成立,
即對![]() ,
,![]() 恒成立.
恒成立.
設函數![]() ,
,![]()
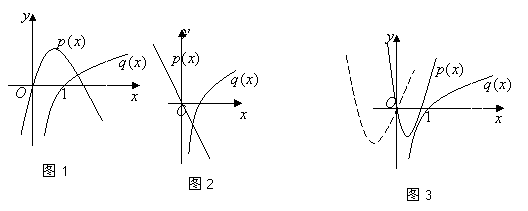
(1)如圖1,當![]() 時,即
時,即![]() ,函數
,函數![]() 為開口向下的二次函數,
為開口向下的二次函數,
則當![]() 時,函數
時,函數![]() 的圖象在
的圖象在![]() 的圖象上方是不可能的;
的圖象上方是不可能的;
(2)如圖2,當![]() 時,即
時,即![]() ,對于
,對于![]() 的函數
的函數![]() 的圖象恒在
的圖象恒在![]() 的圖象上方;
的圖象上方;
(3)如圖3,當![]() 時,即
時,即![]() ,函數
,函數![]() 為過坐標原點且開口向上的二次函數,要使
為過坐標原點且開口向上的二次函數,要使![]() 的函數
的函數![]() 的圖象恒在
的圖象恒在![]() 的圖象上方,只需函數
的圖象上方,只需函數![]() 的圖象與
的圖象與![]() 軸的交點不在
軸的交點不在![]() 的右邊,即
的右邊,即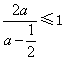 ,則
,則![]() ,且
,且![]() ,即
,即![]() .
.
綜上可知當![]() 時,對
時,對![]() 的函數
的函數![]() 的圖象恒在
的圖象恒在![]() 的圖象上方,即當
的圖象上方,即當![]() 時函數
時函數![]() 的圖象恒在直線
的圖象恒在直線![]() 的下方。
的下方。


科目:高中數學 來源: 題型:
(09年濟寧質檢一理)(14分)
已知數列![]() 的前
的前![]() 項和為
項和為![]() ,對一切正整數
,對一切正整數![]() ,點
,點![]() 都在函數
都在函數![]() 的圖象上,且在點
的圖象上,且在點![]() 處的切線的斜率為
處的切線的斜率為![]() .
.
(Ⅰ)求數列![]() 的通項公式;
的通項公式;
(Ⅱ)若![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(Ⅲ)設![]() ,
,![]() ,等差數列
,等差數列![]() 的任一項
的任一項![]() ,其中
,其中![]() 是
是![]() 中最小的數,
中最小的數,![]() ,求數列
,求數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
(09年濟寧質檢一理)(12分)
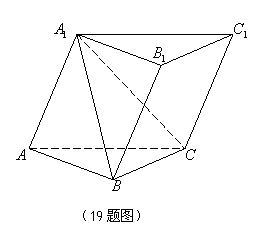
如圖,在三棱柱![]() 中,所有的棱長都為2,
中,所有的棱長都為2,![]() .
.
(Ⅰ)求證:![]() ;
;
(Ⅱ)當三棱柱![]() 的體積最大時,求平面
的體積最大時,求平面![]() 與平面
與平面![]() 所成的銳角的余弦值.
所成的銳角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
(09年濟寧質檢一理)(12分)
某甲有一個放有3個紅球、2個白球、1個黃球共6個球的箱子;某乙也有一個放有3個紅球、2個白球、1個黃球共6個球的箱子.
(Ⅰ)若甲在自己的箱子里任意取球,取后不放回,每次只取一個球,直到取到紅球為止,求甲取球次數![]() 的數學期望;
的數學期望;
(Ⅱ)若甲、乙兩人各從自己的箱子里任取一球比顏色,規定同色時為甲勝,異色時為乙勝,這個游戲規則公平嗎?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com