
在一般情況下,大橋上的車流速度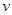 (單位:千米/小時)是車流密度
(單位:千米/小時)是車流密度 (單位:輛/千米)的函數.當橋上的車流密度達到
(單位:輛/千米)的函數.當橋上的車流密度達到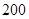 輛/千米時,造成堵塞,此時車流速度為
輛/千米時,造成堵塞,此時車流速度為 ;當
;當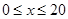 時,車流速度為
時,車流速度為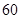 千米/小時.研究表明:當
千米/小時.研究表明:當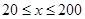 時,車流速度
時,車流速度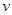 是車流密度
是車流密度 的一次函數.
的一次函數.
(1)當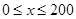 時,求函數
時,求函數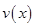 的表達式;
的表達式;
(2)當車流密度 為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)
為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)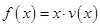 可以達到最大,并求出最大值.(精確到1輛/小時)
可以達到最大,并求出最大值.(精確到1輛/小時)
(1)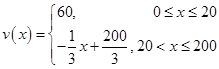 ;
;
(2)當車流密度為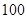 輛/千米時,車流量達到最大,且最大值約
輛/千米時,車流量達到最大,且最大值約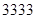 輛/小時.
輛/小時.
解析試題分析:(1)先根據題中函數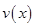 在區間
在區間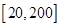 上為一次函數,設
上為一次函數,設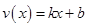 ,利用
,利用 和
和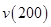 的值列方程組解出
的值列方程組解出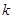 和
和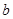 的值,從而確定函數
的值,從而確定函數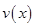 的解析式;(2)利用(1)中函數
的解析式;(2)利用(1)中函數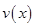 的解析式,將函數
的解析式,將函數 的解析式確定下來(分段函數),然后分別求出函數
的解析式確定下來(分段函數),然后分別求出函數 在區間
在區間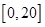 與
與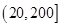 上的最大值,并比較大小,從而確定函數
上的最大值,并比較大小,從而確定函數 在定義域
在定義域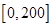 的最大值,進而確定相應的車流密度與車流量.
的最大值,進而確定相應的車流密度與車流量.
試題解析:(1)當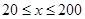 時,設
時,設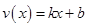 ,
,
則有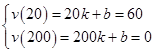 ,解得
,解得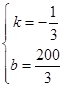 ,
,
所以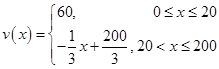 ;
;
(2)由題意知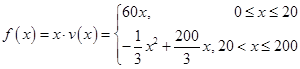 ,
,
當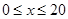 時,
時,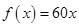 ,則函數
,則函數 在區間
在區間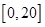 上單調遞增,此時
上單調遞增,此時 在
在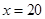 處取最大值,
處取最大值,
即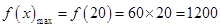 ;
;
當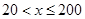 時,
時,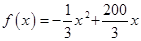 ,函數圖象開口朝上,對稱軸為直線
,函數圖象開口朝上,對稱軸為直線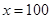 ,
,
此時函數 在
在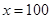 處取得最大值,即
處取得最大值,即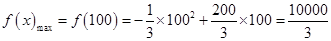 ,
,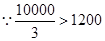 ,故當
,故當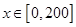 時,
時,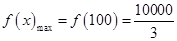 ,
,
即當車流密度為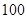 輛/千米時,車流量達到最大,且最大值約
輛/千米時,車流量達到最大,且最大值約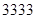 輛/小時.
輛/小時.
考點:1.函數解析式;2.分段函數的最值


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
一企業生產的某產品在不做電視廣告的前提下,每天銷售量為b噸.經市場調查后得到如下規律:若對產品進行電視廣告的宣傳,每天的銷售量S(噸)與電視廣告每天的播放量n(次)的關系可用如圖所示的程序框圖來體現.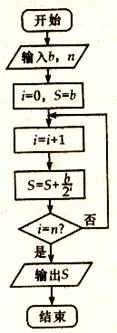
(1)試寫出該產品每天的銷售量S(噸)關于電視廣告每天的播放量n(次)的函數關系式;
(2)要使該產品每天的銷售量比不做電視廣告時的銷售量至少增加90%,則每天電視廣告的播放量至少需多少次?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某社區有甲、乙兩家乒乓球俱樂部,兩家設備和服務都很好,但收費方式不同.甲家每張球臺每小時5元;乙家按月計費,一個月中30小時以內(含30小時)每張球臺90元,超過30小時的部分每張球臺每小時2元.小張準備下個月從這兩家中的一家租一張球臺開展活動,其活動時間不少于15小時,也不超過40小時.
(1)設在甲家租一張球臺開展活動 小時的收費為
小時的收費為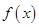 元
元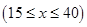 ,在乙家租一張球臺開展活動
,在乙家租一張球臺開展活動 小時的收費為
小時的收費為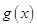 元
元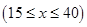 .試求
.試求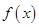 和
和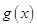 .
.
(2)問:小張選擇哪家比較合算?為什么?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com