中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情
在雙曲線=－1的一支上有不同的三點A(x1,y1),B(x2,6),C(x3,y3),與焦點F(0,5)的距離成等差數列.

(1)求y1+y3的值;

(2)求證:線段AC的垂直平分線經過某一定點,并求出定點坐標.

(1)解:∵=e,∴|PF|=ey－a.

又A、B、C到F的距離成等差數列,

∴2(ey2－a)=(ey1－a)+(ey3－a).

∴y1+y3=2y2=12.

(2)證明:由題意,得

①－②,得(y1－y3)(y1+y3)－(x1－x3)(x1+x3)=0.

∴.

若x1+x3=0,則kAC=0,y1=y3=y2=6,A、B、C三點共線,這是不可能的.

∴x1+x3≠0.則AC的中垂線方程為

y－6=－(x－),即y=－.

因此,AC的中垂線過定點(0,).


練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

在雙曲線
y2
12
-
x2
13
=1的一支上不同的三點A（x1，y1）、B（
26
，6）、C（x2，y2）與焦點F（0，5）的距離成等差數列．
（1）求y1+y2；
（2）證明線段AC的垂直平分線經過某一定點，并求該定點的坐標．

查看答案和解析>>

科目：高中數學 來源： 題型：

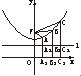精英家教網如圖，在雙曲線
y2
12
-
x2
13
=1的上支上有三點A（x1，y1），B（x2，6），C（x3，y3），它們與點F（0，5）的距離成等差數列．
（1）求y1+y3的值；
（2）證明：線段AC的垂直平分線經過某一定點，并求此點坐標．

查看答案和解析>>

科目：高中數學 來源：高三數學教學與測試 題型：044

在雙曲線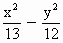＝－1的一支上有不同三點A，6)，C()與焦點F(0，5)的距離成等差數列，(1)求；(2)求證線段AC的垂直平分線經過某一定點，并求出定點的坐標．

查看答案和解析>>

科目：高中數學 來源：黃岡新內參·高考（專題）模擬測試卷·數學 題型：044

在雙曲線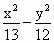＝－1的一支上有不同的三點A(，)，B(，6)，C(，)與焦點F(0，5)的距離成等差數列．

(1)求

(2)求證：線段AC的垂直平分線經過某一定點，并求出定點的坐標．

查看答案和解析>>

科目：高中數學 來源：高考零距離　二輪沖刺優化講練　數學 題型：044

在雙曲線－＝1的一支上有三個不同的點A(x1，y1)、B(，6)、C(x2，y2)，它們與焦點F(0，5)的距離成等差數列，求y1＋y2的值．

查看答案和解析>>

同步練習冊答案