科目：高中數學 來源： 題型：解答題
如圖所示，空間中有一直角三角形
，
為直角，
，
，現以其中一直角邊
為軸，按逆時針方向旋轉
后，將
點所在的位置記為
，再按逆時針方向繼續旋轉
后，點所在的位置記為
.
（1）連接
，取的中點為
，求證：面
面
；
（2）求
與平面所成的角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
如圖，三棱柱ABC－A1B1C1的底面是邊長為2的正三角形且側棱垂直于底面，側棱長是
，D是AC的中點．
（1）求證：B1C∥平面A1BD；
（2）求二面角A1－BD－A的大小；
（3）求直線AB1與平面A1BD所成的角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
如圖，在四棱錐P—ABCD中，底面ABCD為直角梯形，AD∥BC，∠ADC＝90°，平面PAD⊥底面ABCD，Q為AD的中點，M是棱PC上的點，PA＝PD＝2，BC＝
AD＝1，CD＝
.
(1)若點M是棱PC的中點，求證：PA∥平面BMQ；
(2)若二面角M—BQ—C為30°，設PM＝tMC，試確定t的值．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
如圖所示，PA⊥平面ABC，點C在以AB為直徑的⊙O上，∠CBA＝30°，PA＝AB＝2，點E為線段PB的中點，點M在弧AB上，且OM∥AC.
(1)求證：平面MOE∥平面PAC.
(2)求證：平面PAC⊥平面PCB.
(3)設二面角M—BP—C的大小為θ，求cos θ的值．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
如圖,在斜三棱柱
中,側面
⊥底面
,側棱
與底面成60°的角,
.底面是邊長為2的正三角形,其重心為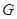
點,
是線段
上一點,且
.
(1)求證:
//側面;
(2)求平面
與底面所成銳二面角的余弦值;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
中，
，
，
，
，
，E為CD上一點，
，
；
到平面
的距離。
的大小為
，菱形
在面
內，
兩點在棱
上，
，
是
的中點，
面
，垂足為
.
平面
；
與
所成角的余弦值.
中，側棱
底面
,
為
的中點,
,
.
平面
；
的體積.
中，底面
是正方形，
，
，點
在
上，且
.
平面
的余弦值；
上存在點
，使
∥平面
，并求
的長.