
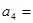 ;
;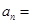 .
.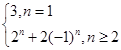 .
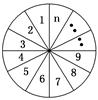
.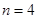 時,第1區域有3種選擇, 第2區域有2種選擇,第3區域有2種選擇,因為第4區域要與第1區域顏色不同,故對第3區域的選擇分類討論:當第3區域與第1區域顏色相同時,第4區域有2種選擇;當第3區域與第1區域顏色不同時,第4區域僅有1種選擇.所以
時,第1區域有3種選擇, 第2區域有2種選擇,第3區域有2種選擇,因為第4區域要與第1區域顏色不同,故對第3區域的選擇分類討論:當第3區域與第1區域顏色相同時,第4區域有2種選擇;當第3區域與第1區域顏色不同時,第4區域僅有1種選擇.所以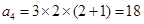 ;(2)當將圓分成n個區域,用3種不同顏色給每一個區域染色時,第1區域有3種染色方案,第2區域至第
;(2)當將圓分成n個區域,用3種不同顏色給每一個區域染色時,第1區域有3種染色方案,第2區域至第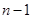 區域有2種染色方案.此時考慮第
區域有2種染色方案.此時考慮第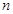 區域也有2種涂色方案,在此情況下有兩種情況:
區域也有2種涂色方案,在此情況下有兩種情況: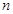 區域與第1區域同色,此時相當將這兩區域重合,這時問題轉化為3種不同顏色給圓上
區域與第1區域同色,此時相當將這兩區域重合,這時問題轉化為3種不同顏色給圓上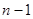 個區域涂色,即為
個區域涂色,即為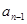 種染色方案;
種染色方案;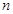 區域與第1區域不同色,此時問題就轉化為用3種不同顏色給圓上
區域與第1區域不同色,此時問題就轉化為用3種不同顏色給圓上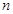 個區域染色,且相鄰區域顏色互異,即此時的情況就是
個區域染色,且相鄰區域顏色互異,即此時的情況就是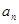 .根據分類原理可知
.根據分類原理可知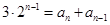 ,且滿足初始條件:
,且滿足初始條件: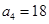 .
.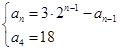 ,由
,由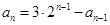 變形得
變形得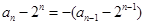 ,所以數列
,所以數列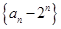 是以-1為公比的等比數列.所以
是以-1為公比的等比數列.所以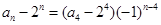 ,即
,即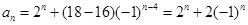 .當
.當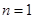 時,易知有3種染色方法,即
時,易知有3種染色方法,即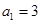 ,不滿足上述通項公式;當
,不滿足上述通項公式;當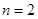 時,易知有
時,易知有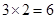 種染色方法,即
種染色方法,即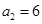 ,滿足上述通項公式;當
,滿足上述通項公式;當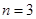 時,易知有
時,易知有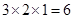 種染色方法,即
種染色方法,即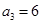 ,滿足上述通項公式.
,滿足上述通項公式.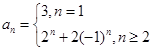 .
.

科目:高中數學 來源:不詳 題型:解答題
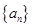 滿足:
滿足: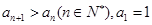 ,該數列的前三項分別加上l,l,3后順次成為等比數列
,該數列的前三項分別加上l,l,3后順次成為等比數列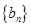 的前三項.
的前三項.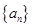 ,
,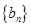 的通項公式;
的通項公式;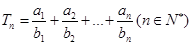 ,若
,若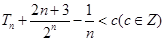 恒成立,求c的最小值.
恒成立,求c的最小值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com