
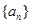 的前n項和為
的前n項和為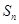 ,已知
,已知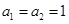 ,
,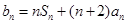 ,數列
,數列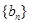 是公差為d的等差數列,
是公差為d的等差數列,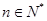 .
.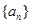 的通項公式;
的通項公式;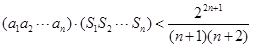 .
. ;(3)參考解析.
;(3)參考解析.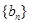 是一個等差數列,通過列舉前兩項的值可求得數列
是一個等差數列,通過列舉前兩項的值可求得數列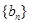 的公差.(2)通過求出
的公差.(2)通過求出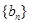 的通項公式就得到一個關于
的通項公式就得到一個關于 的關系式.這類題型一般都是通過向前遞推一個等式然后求差利用
的關系式.這類題型一般都是通過向前遞推一個等式然后求差利用 ,(
,( ),再根據兩式相減后的結果累乘即可求得
),再根據兩式相減后的結果累乘即可求得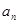 的通項.(3)由要證明的不等式的左邊可觀察要找到一個關于
的通項.(3)由要證明的不等式的左邊可觀察要找到一個關于 的式子.并且再進一步放大. 通過
的式子.并且再進一步放大. 通過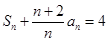 可得到
可得到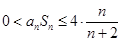 .再通過累乘即可得到要證的結果.最要注明等號不成立,是由于
.再通過累乘即可得到要證的結果.最要注明等號不成立,是由于 .本題是數列知識的綜合題,涉及數列的通項公式,數列的求和常見的解題方法.結合不等式知識.雖然不等式的證明僅僅是應用了基本不等式的知識,但是包含重新組合不等式左邊的結構的思維很妙.同時取不到等號
.本題是數列知識的綜合題,涉及數列的通項公式,數列的求和常見的解題方法.結合不等式知識.雖然不等式的證明僅僅是應用了基本不等式的知識,但是包含重新組合不等式左邊的結構的思維很妙.同時取不到等號 .通過檢驗n=1來說明,感覺四兩撥千斤的味道.
.通過檢驗n=1來說明,感覺四兩撥千斤的味道. ,
,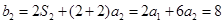 .
. .
.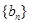 是等差數列.所以
是等差數列.所以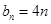 .所以
.所以 .即
.即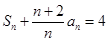 . ①當
. ①當 時.
時. 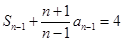 .. ②.由①-②得.
.. ②.由①-②得.  .所以
.所以 .即
.即 .則
.則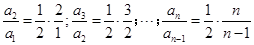 .以上各式相乘得.
.以上各式相乘得.  .又因為
.又因為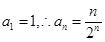 .
.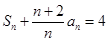 .
. .所以
.所以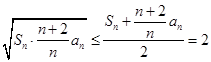 .則
.則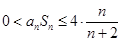 .所以
.所以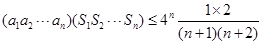 . ③.因為n=1時
. ③.因為n=1時 .所以③式等號不成立.則
.所以③式等號不成立.則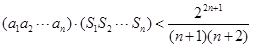 .
.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com