
已知橢圓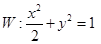 ,直線
,直線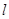 與
與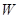 相交于
相交于 、
、 兩點,
兩點,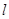 與
與 軸、
軸、 軸分別相交于
軸分別相交于 、
、 兩點,
兩點, 為坐標原點.
為坐標原點.
(1)若直線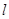 的方程為
的方程為 ,求
,求 外接圓的方程;
外接圓的方程;
(2)判斷是否存在直線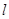 ,使得
,使得 、
、 是線段
是線段 的兩個三等分點,若存在,求出直線
的兩個三等分點,若存在,求出直線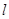 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
(1) ;(2)存在,且直線
;(2)存在,且直線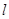 的方程為
的方程為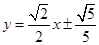 或
或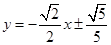 .
.
解析試題分析:(1)先確定 三個頂點的坐標,利用其外接圓圓心即為該三角形垂直平分線的交點求出外接圓的圓心,并利用兩點間的距離公式求出外接圓的半徑,從而求出外接圓的方程;(2)將
三個頂點的坐標,利用其外接圓圓心即為該三角形垂直平分線的交點求出外接圓的圓心,并利用兩點間的距離公式求出外接圓的半徑,從而求出外接圓的方程;(2)將 、
、 是線段
是線段 的兩個三等分點等價轉化為線段
的兩個三等分點等價轉化為線段 的中點與線段
的中點與線段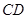 的中點重合,且有
的中點重合,且有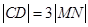 ,借助韋達定理與弦長公式進行求解.
,借助韋達定理與弦長公式進行求解.
試題解析:(1)因為直線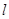 的方程為
的方程為 ,
,
所以 軸的交點
軸的交點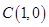 ,與
,與 軸的交點
軸的交點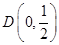 .
.
則線段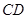 的中點
的中點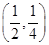 ,
,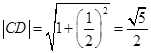 ,
,
即 外接圓的圓心為
外接圓的圓心為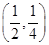 ,半徑為
,半徑為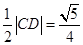 ,
,
所以 外接圓的方程為
外接圓的方程為 ;
;
(2)結論:存在直線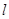 ,使得
,使得 、
、 是線段
是線段 的兩個三等分點.
的兩個三等分點.
理由如下:
由題意,設直線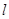 的方程為
的方程為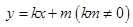 ,
,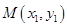 ,
,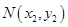 ,
,
則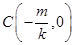 ,
,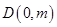 ,
,
由方程組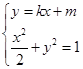 得
得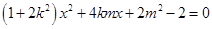 ,
,
所以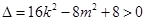 ,(*)
,(*)
由韋達定理,得 ,
,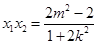 .
.
由 、
、 是線段
是線段 的兩個三等分點,得線段
的兩個三等分點,得線段 的中點與線段
的中點與線段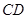 的中點重合.
的中點重合.
所以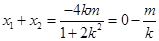 ,
,
解得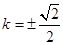 .
.
由 、
、 是線段
是線段 的兩個三等分點,得
的兩個三等分點,得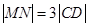 .
.
所以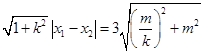 ,
,
即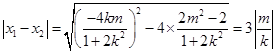 ,
,
解得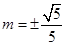 .
.
驗證知(*)成立.
所以存在直線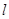 ,使得
,使得 、
、 是線段
是線段 的兩個三等分點,此時直線l的方程為
的兩個三等分點,此時直線l的方程為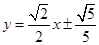 ,
,
或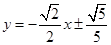 .
.
考點:1.三角形的外接圓方程;2.韋達定理;3.弦長公式


科目:高中數學 來源: 題型:解答題
已知頂點為原點 的拋物線
的拋物線 的焦點
的焦點 與橢圓
與橢圓 的右焦點重合,
的右焦點重合, 與
與 在第一和第四象限的交點分別為
在第一和第四象限的交點分別為 .
.
(1)若 是邊長為
是邊長為 的正三角形,求拋物線
的正三角形,求拋物線 的方程;
的方程;
(2)若 ,求橢圓
,求橢圓 的離心率
的離心率 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知拋物線C的頂點在原點,開口向右,過焦點且垂直于拋物線對稱軸的弦長為2,過C上一點A作兩條互相垂直的直線交拋物線于P,Q兩點. 
(1)若直線PQ過定點 ,求點A的坐標;
,求點A的坐標;
(2)對于第(1)問的點A,三角形APQ能否為等腰直角三角形?若能,試確定三角形APD的個數;若不能,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知橢圓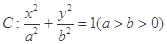 的離心率為
的離心率為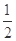 ,以原點
,以原點 為圓心,橢圓的短半軸長為半徑的圓與直線
為圓心,橢圓的短半軸長為半徑的圓與直線 相切。
相切。
(1)求橢圓 的標準方程;
的標準方程;
(2)若直線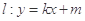 與橢圓
與橢圓 相交于
相交于 、
、 兩點,且
兩點,且 ,試判斷
,試判斷 的面積是否為定值?若為定值,求出定值;若不為定值,說明理由.
的面積是否為定值?若為定值,求出定值;若不為定值,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
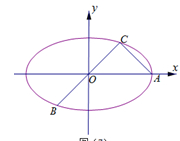
如圖所示,已知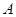 、
、 、
、 是長軸長為
是長軸長為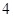 的橢圓
的橢圓 上的三點,點
上的三點,點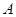 是長軸的一個端點,
是長軸的一個端點, 過橢圓中心
過橢圓中心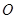 ,且
,且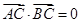 ,
,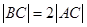 .
.
(1)求橢圓 的方程;
的方程;
(2)在橢圓 上是否存點
上是否存點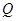 ,使得
,使得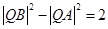 ?若存在,有幾個(不必求出
?若存在,有幾個(不必求出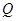 點的坐標),若不存在,請說明理由;
點的坐標),若不存在,請說明理由;
(3)過橢圓 上異于其頂點的任一點
上異于其頂點的任一點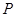 ,作圓
,作圓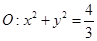 的兩條線,切點分別為
的兩條線,切點分別為 、
、 ,,若直線
,,若直線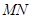 在
在 軸、
軸、 軸上的截距分別為
軸上的截距分別為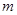 、
、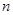 ,證明:
,證明: 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知橢圓 的短半軸長為
的短半軸長為 ,動點
,動點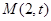
 在直線
在直線 (
( 為半焦距)上.
為半焦距)上.
(1)求橢圓的標準方程;
(2)求以 為直徑且被直線
為直徑且被直線 截得的弦長為
截得的弦長為 的圓的方程;
的圓的方程;
(3)設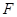 是橢圓的右焦點,過點
是橢圓的右焦點,過點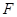 作
作 的垂線與以
的垂線與以 為直徑的圓交于點
為直徑的圓交于點 ,
,
求證:線段 的長為定值,并求出這個定值.
的長為定值,并求出這個定值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知拋物線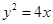 .
.
(1)若圓心在拋物線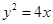 上的動圓,大小隨位置而變化,但總是與直線
上的動圓,大小隨位置而變化,但總是與直線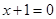 相切,求所有的圓都經過的定點坐標;
相切,求所有的圓都經過的定點坐標;
(2)拋物線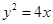 的焦點為
的焦點為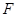 ,若過
,若過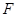 點的直線與拋物線相交于
點的直線與拋物線相交于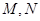 兩點,若
兩點,若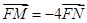 ,求直線
,求直線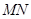 的斜率;
的斜率;
(3)若過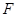 點且相互垂直的兩條直線
點且相互垂直的兩條直線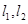 ,拋物線與
,拋物線與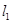 交于點
交于點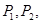 與
與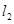 交于點
交于點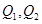 .
.
證明:無論如何取直線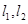 ,都有
,都有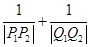 為一常數.
為一常數.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
拋物線頂點在原點,它的準線過雙曲線 =1(a>0,b>0)的一個焦點,并與雙曲線實軸垂直,已知拋物線與雙曲線的一個交點為
=1(a>0,b>0)的一個焦點,并與雙曲線實軸垂直,已知拋物線與雙曲線的一個交點為 ,求拋物線與雙曲線方程.
,求拋物線與雙曲線方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com