

| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
| CD |
| DB |
| CD |
| AB |
| AC |
A、
| ||
B、
| ||
| C、1 | ||
| D、0 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 (2010•江蘇二模)如圖是一塊長(zhǎng)方形區(qū)域ABCD,AD=2(km),AB=1(km).在邊AD的中點(diǎn)O處,有一個(gè)可轉(zhuǎn)動(dòng)的探照燈,其照射角∠EOF始終為
(2010•江蘇二模)如圖是一塊長(zhǎng)方形區(qū)域ABCD,AD=2(km),AB=1(km).在邊AD的中點(diǎn)O處,有一個(gè)可轉(zhuǎn)動(dòng)的探照燈,其照射角∠EOF始終為| π |
| 4 |
| 3π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 6 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2012學(xué)年浙江省杭州七校高一第二學(xué)期期中聯(lián)考數(shù)學(xué)試卷(解析版) 題型:解答題
在 中,滿足
中,滿足 ,
, 是
是 邊上的一點(diǎn).
邊上的一點(diǎn).
(Ⅰ)若 ,求向量
,求向量 與向量
與向量 夾角的正弦值;
夾角的正弦值;
(Ⅱ)若 ,
, =m (m為正常數(shù)) 且
=m (m為正常數(shù)) 且 是
是 邊上的三等分點(diǎn).,求
邊上的三等分點(diǎn).,求 值;
值;
(Ⅲ)若 且
且 求
求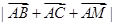 的最小值。
的最小值。
【解析】第一問(wèn)中,利用向量的數(shù)量積設(shè)向量 與向量
與向量 的夾角為
的夾角為 ,則
,則
令 =
= ,得
,得 ,又
,又 ,則
,則 為所求
為所求
第二問(wèn)因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912192026514838/SYS201207091220070463574796_ST.files/image008.png">, =m所以
=m所以 ,
,
(1)當(dāng) 時(shí),則
時(shí),則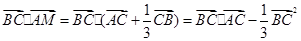 =
=
(2)當(dāng) 時(shí),則
時(shí),則 =
=
第三問(wèn)中,解:設(shè) ,因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912192026514838/SYS201207091220070463574796_ST.files/image029.png">
,因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912192026514838/SYS201207091220070463574796_ST.files/image029.png"> ,
, ;
;
所以 即
即 于是
于是 得
得
從而
運(yùn)用三角函數(shù)求解。
(Ⅰ)解:設(shè)向量 與向量
與向量 的夾角為
的夾角為 ,則
,則
令 =
= ,得
,得 ,又
,又 ,則
,則 為所求……………2分
為所求……………2分
(Ⅱ)解:因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912192026514838/SYS201207091220070463574796_ST.files/image008.png">, =m所以
=m所以 ,
,
(1)當(dāng) 時(shí),則
時(shí),則 =
= ;-2分
;-2分
(2)當(dāng) 時(shí),則
時(shí),則 =
= ;--2分
;--2分
(Ⅲ)解:設(shè) ,因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912192026514838/SYS201207091220070463574796_ST.files/image029.png">
,因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912192026514838/SYS201207091220070463574796_ST.files/image029.png"> ,
, ;
;
所以 即
即 于是
于是 得
得
從而 ---2分
---2分
= =
=
= …………………………………2分
…………………………………2分
令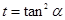 ,
, 則
則 ,則函數(shù)
,則函數(shù) ,在
,在 遞減,在
遞減,在 上遞增,所以
上遞增,所以 從而當(dāng)
從而當(dāng) 時(shí),
時(shí),
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2010-2011年浙江省高二下學(xué)期期中考試數(shù)學(xué)理卷 題型:填空題
在平面上,設(shè)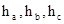 是三角形
是三角形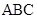 三條邊上的高.P為三角形內(nèi)任一點(diǎn),P到相應(yīng)三邊的距離分別為
三條邊上的高.P為三角形內(nèi)任一點(diǎn),P到相應(yīng)三邊的距離分別為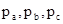 ,我們可以得到結(jié)論:
,我們可以得到結(jié)論:
試通過(guò)類(lèi)比,寫(xiě)出在空間中的類(lèi)似結(jié)論____________________________.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com