Question

(理)已知曲線C:f(x)=x²,C上點A、A_n的橫坐標分別為1和a_n(n∈N^*),且a₁=5,x_n+1=af(x_n-1)+1(a＞0,a≠,a≠1).記區間D_n=［1,a_n］(a_n＞1).當x∈D_n時,曲線C上存在點P_n(x_n,f(x_n)),使得點P_n處的切線與直線AA_n平行.

(1)試判斷:數列{log_a(x_n-1)+1}是什么數列;

(2)當D_nD_n+1對一切n∈N^*恒成立時,求實數a的取值范圍;

(3)記數列{a_n}的前n項和為S_n,當a=時,試比較S_n與n+7的大小,并說明你的結論.

(文)已知f(x)=ax³+bx²+cx+d(a≠0)是定義在R上的函數,其圖象交x軸于A、B、C三點.若點B的坐標為(2,0),且f(x)在［-1,0］和［4,5］上有相同的單調性,在［0,2］和［4,5］上有相反的單調性.

(1)求c的值.

(2)在函數f(x)的圖象上是否存在一點M(x₀,y₀),使得f(x)在點M處的切線斜率為3b?若存在,求出點M的坐標;若不存在,請說明理由.

(3)求|AC|的取值范圍.

Answer 1

答案：(理)解:(1)是等比數列.2分由點P_n處的切線與直線AA_n平行可知,x_n=.

由x_n+1=af(x_n-1)+1(a＞0,a≠,a≠1)可知x_n+1-1=a(x_n-1)²,則log_a(x_n+1-1)=2log_a(x_n-1)+1.設b_n=log_a(x_n-1),則b_n+1+1=2(b_n+1).又b₁=log_a(x₁-1)=log_a2,因此數列{b_n+1}是以b₁+1為首項,2為公比的等比數列,即{log_a(x_n-1)+1}是等比數列.

則b_n+1=(log_a2+1)·2^n-1,即b_n=(log_a2+1)·2^n-1-1=log_a,∴x_n=1+.

(2)由條件x_n=可知a_n=1+.由D_nD_n+1知a_n＞a_n+1,即 ［1-］＞0,則［1-］＞0,即0＜a＜.

(3)數列{a_n}的前n項和S_n,當a=時,a_n=1+=1+8.

S_n=n+8［+()²+()⁴+…+］.可以證明:當n≥4,有2^n-1＞n+1;∴當n≤3時,S_n≤n+8［+()²+()⁴］=n+＜n+7;

當n≥4時,S_n＜n+8［+()²+()⁴+()⁵+()⁶+…+()ⁿ⁺¹］=n+7-()^n-2＜n+7,則S_n＜n+7.

(文)解：(1)∵f(x)在［-1,0］和［0,2］上有相反的單調性,∴x=0是f(x)的一個極值點.故f′(0)=0,2分即3ax²+2bx+c=0有一個解x=0,則c=0.

(2)∵f(x)交x軸于點B(2,0),∴8a+4b+d=0,即d=-4(b+2a).令f′(x)=0得3ax²+2bx=0,x₁=0,x₂=.

∵f(x)在［0,2］和［4,5］上有相反的單調性,∴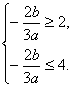∴-6≤≤-3.

假設存在點M(x₀,y₀),使得f(x)在點M處的切線斜率為3b,則f′(x₀)=3b,即3ax₀²+2bx₀-3b=0.

∵Δ=(2b)²-4×3a×(-3b)=4b²+36ab=4ab(+9),而-6≤≤-3,∴Δ＜0.故不存在點M(x₀,y₀),使得f(x)在點M處的切線斜率為3b.

(3)設A(α,0),C(β,0),依題意可令f(x)=a(x-α)(x-2)(x-β)=a［x³-(2+α+β)x²+(2α+2β+αβ)x-2αβ］,

則即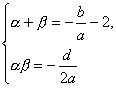∴|AC|=|α-β|=

==.〔∵d=-4(b+2a)〕∵-6≤≤-3,∴當=-6時,|AC|_max=;當=-3時,|AC|_min=3.故3≤|AC|≤.