中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

如圖,拋物線E:y2=4x的焦點為F,準線l與x軸的交點為A.點C在拋物線E上,以C為圓心,|CO|為半徑作圓,設圓C與準線l交于不同的兩點M,N.

(1)若點C的縱坐標為2,求|MN|;

(2)若|AF|2=|AM|·|AN|,求圓C的半徑.

 

【答案】

（1）2 （2）

【解析】

解:(1)拋物線y2=4x的準線l的方程為x=-1.

由點C的縱坐標為2,點C在拋物線E上,

得點C的坐標為(1,2),

所以點C到準線l的距離d=2,

又|CN|=|CO|=,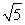

所以|MN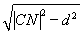|=2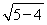=2=2.

(2)設C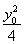（,y0）,

則圓C的方程為（x-）2+(y-y0)2=+,

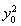即x2-x+y2-2y0y=0.

由x=-1,

得y2-2y0y+1+=0,

設M(-1,y1),N(-1,y2),則

由|AF|2=|AM|·|AN|,

得|y1y2|=4,

所以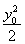+1=4,

解得y0=±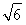,此時Δ>0.

所以圓心C的坐標為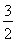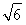（,）或（,-）,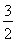

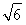從而|CO|2=,

|CO|=,

即圓C的半徑為.

 

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

精英家教網如圖，已知直線l與拋物線x2=4y相切于點P（2，1），且與x軸交于點A，O為坐標原點，定點B的坐標為（2，0）．
（1）若動點M滿足
AB
•
BM
+
2
|
AM
|=0，求動點M的軌跡Q；
（2） F1，F2是軌跡Q的左、右焦點，過F1作直線l（不與x軸重合），l與軌跡Q相交于C，D，并與圓x2+y2=3相交于E，F．當
F2E
•
F2F
=λ，且λ∈[
2
3
，1]時，求△F2CD的面積S的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：

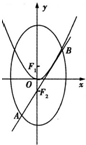如圖所示，橢圓C：
 x2   
b2
+
y2    
a2
=1(a＞b＞0)的焦點為F1（0，c），F2（0，-c）（c＞0），拋物線x2=2py（p＞0）的焦點與F1重合，過F2的直線l與拋物線P相切，切點在第一象限，且與橢圓C相交于A，B兩點，且
F2B
=λ
AF2
．
（1）求證：切線l的斜率為定值；
（2）當λ∈[2，4]時，求橢圓的離心率e的取值范圍．

查看答案和解析>>

科目：高中數學 來源：2013-2014學年人教版高考數學文科二輪專題復習提分訓練24練習卷（解析版） 題型：解答題

如圖所示,已知拋物線E:y2=x與圓M:(x-4)2+y2=r2(r>0)相交于A、B、C、D四個點.

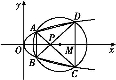
(1)求r的取值范圍;

(2)當四邊形ABCD的面積最大時,求對角線AC、BD的交點P的坐標.

 

查看答案和解析>>

科目：高中數學 來源：2013年黑龍江省高三第四次聯考理科數學試卷（解析版） 題型：解答題

已知拋物線E:y2= 4x，點P（2，O）．如圖所示，直線．過點P且與拋物線E交于A（xl，y1）、B（ x2，y2）兩點，直線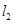過點P且與拋物線E交于C（x3， y3）、D（x4，y4）兩點．過點P作x軸的垂線，與線段AC和BD分別交于點M、N．

（I）求y1y2的值；

（Ⅱ）求訌：|PM|="|" PN|

 

查看答案和解析>>

同步練習冊答案