
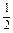 )為偶函數.
)為偶函數.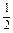 )為偶函數,只需證明其對稱軸為x=0.
)為偶函數,只需證明其對稱軸為x=0. -
-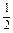 ="0."
="0." 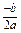 -1與拋物線的對稱軸x=
-1與拋物線的對稱軸x=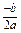 關于y軸對稱.
關于y軸對稱.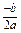 -1=-
-1=-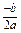 .
.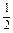 )為偶函數.
)為偶函數.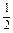 ),
),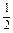 )=f(x+
)=f(x+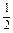 ),(中途結果).
),(中途結果).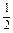 )="f" [-(x-
)="f" [-(x-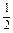 )]
)]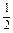 )+1]="f" (x+
)+1]="f" (x+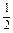 )(中途結果).
)(中途結果).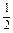 )為偶函數.
)為偶函數.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com