，是否存在不小于2的正整數
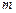，使得對于任意的正整數
都能被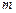整除？如果存在，求出最大的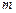值；如果不存在，請說明理由．
挑戰100單元檢測試卷系列答案科目：高中數學 來源：不詳 題型：單選題
,
,
中恰有一個偶數”正確的反設為（ ）| A．，，中至少有兩個偶數 | B．，，中至少有兩個偶數或都是奇數 |
| C．，，都是奇數 | D．，，都是偶數 |
查看答案和解析>>
科目：高中數學 來源：不詳 題型：解答題
，對任意
均滿足
，當且僅當
時等號成立。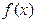
∈M，試比較
與
大小.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，證明見解析
，
，
，
，
，由此猜想
時，
顯然能被36整除．
時，
能被36整除，即
能被36整除．
時，
，
由假設知
能被36整除，
是偶數，
也能被36整除．
都成立．
的最大值為36．
.
；
為
的一個極值點，證明
.
，(其中
為虛數單位)
是純虛數時，求實數
的值；
)為偶函數.
，用
表示線段
上除端點外的所有整點（坐標是整數的點）的個數，則
的值是（ ）
,且
恒成立，則
的最大值為（ ）
，
，
。求證
中至少有一個不小于0。