
對于函數(shù) ,若存在實數(shù)對(
,若存在實數(shù)對( ),使得等式
),使得等式 對定義域中的每一個
對定義域中的每一個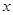 都成立,則稱函數(shù)
都成立,則稱函數(shù) 是“(
是“( )型函數(shù)”.
)型函數(shù)”.
(1) 判斷函數(shù)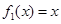 是否為 “(
是否為 “( )型函數(shù)”,并說明理由;
)型函數(shù)”,并說明理由;
(2) 若函數(shù)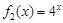 是“(
是“( )型函數(shù)”,求出滿足條件的一組實數(shù)對
)型函數(shù)”,求出滿足條件的一組實數(shù)對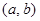 ;
;
(3)已知函數(shù) 是“
是“ 型函數(shù)”,對應(yīng)的實數(shù)對
型函數(shù)”,對應(yīng)的實數(shù)對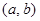 為
為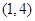 ,當
,當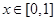 時,
時,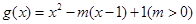 ,若當
,若當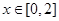 時,都有
時,都有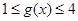 ,試求
,試求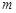 的取值范圍.
的取值范圍.
(1)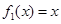 不是“
不是“ 型函數(shù)”,理由詳見解析;(2)
型函數(shù)”,理由詳見解析;(2)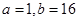 (滿足
(滿足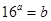 的實數(shù)對
的實數(shù)對 均是正確答案);(3)
均是正確答案);(3)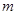 的取值范圍是
的取值范圍是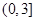 .
.
解析試題分析:(1)根據(jù)條件中的描述,若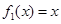 是“
是“ 型函數(shù)”,則需存在實數(shù)
型函數(shù)”,則需存在實數(shù) ,使得
,使得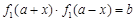 對于任意
對于任意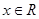 都成立,即
都成立,即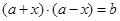 ,
,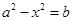 對任意
對任意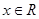 都成立,這顯然是不可能的,因此假設(shè)不成立,即
都成立,這顯然是不可能的,因此假設(shè)不成立,即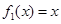 不是“
不是“ 型函數(shù)”;(2)根據(jù)條件描述,
型函數(shù)”;(2)根據(jù)條件描述,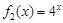 是“
是“ 型函數(shù)”需存在實數(shù)對
型函數(shù)”需存在實數(shù)對 ,使得
,使得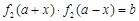 對于任意
對于任意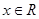 都成立,即
都成立,即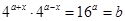 對任意
對任意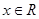 均成立,故所取的實數(shù)對只需滿足等式
均成立,故所取的實數(shù)對只需滿足等式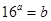 即可,例如
即可,例如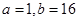 ;
;
(3)根據(jù) 是“
是“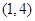 型函數(shù)”可知:
型函數(shù)”可知: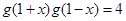 ,即
,即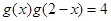 ,而當
,而當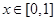 時,
時,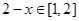 ,故當
,故當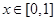 時,若有
時,若有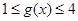 ,必有當
,必有當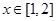 時,
時,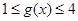 ,因此要使當
,因此要使當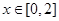 時,都有
時,都有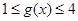 即等價于當
即等價于當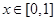 時,
時,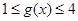 恒成立,因此可以得到不等式
恒成立,因此可以得到不等式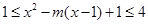 在
在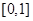 上恒成立,若
上恒成立,若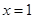 :顯然不等式在
:顯然不等式在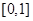 上成立,若
上成立,若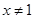 :參變分離后可轉(zhuǎn)化為轉(zhuǎn)化為
:參變分離后可轉(zhuǎn)化為轉(zhuǎn)化為 ,顯然,當
,顯然,當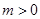 時,不等式(1)成立,而要使不等式(2)成立,
時,不等式(1)成立,而要使不等式(2)成立,
只需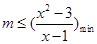 ,通過構(gòu)造函數(shù)令
,通過構(gòu)造函數(shù)令 及
及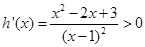 ,可知
,可知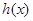 在
在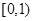 上單調(diào)遞增,故
上單調(diào)遞增,故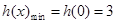 ,因此只需
,因此只需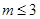 即可從而得到實數(shù)
即可從而得到實數(shù)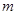 的取值范圍是
的取值范圍是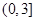 .
.
試題解析:(1)假設(shè)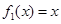 是“(
是“( )型函數(shù)”,則由題意存在實數(shù)對
)型函數(shù)”,則由題意存在實數(shù)對 ,使得
,使得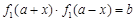 對于任意
對于任意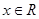 都成立,即
都成立,即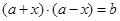 ,
,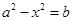 對任意
對任意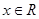 都成立,這顯然是不可能的,因此假設(shè)不成立,即
都成立,這顯然是不可能的,因此假設(shè)不成立,即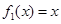 不是
不是

 小學課時作業(yè)全通練案系列答案
小學課時作業(yè)全通練案系列答案 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案科目:高中數(shù)學 來源: 題型:解答題
某人準備租一輛車從孝感出發(fā)去武漢,已知從出發(fā)點到目的地的距離為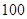
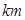 ,按交通法規(guī)定:這段公路車速限制在
,按交通法規(guī)定:這段公路車速限制在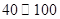 (單位:
(單位: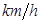 )之間.假設(shè)目前油價為
)之間.假設(shè)目前油價為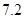 (單位:元
(單位:元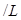 ),汽車的耗油率為
),汽車的耗油率為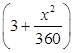 (單位:
(單位: ), 其中
), 其中 (單位:
(單位: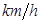 )為汽車的行駛速度,耗油率指汽車每小時的耗油量.租車需付給司機每小時的工資為
)為汽車的行駛速度,耗油率指汽車每小時的耗油量.租車需付給司機每小時的工資為 元,不考慮其它費用,這次租車的總費用最少是多少?此時的車速
元,不考慮其它費用,這次租車的總費用最少是多少?此時的車速 是多少?(注:租車總費用=耗油費+司機的工資)
是多少?(注:租車總費用=耗油費+司機的工資)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)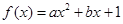 (
( 為實數(shù),
為實數(shù),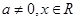 ),
),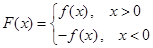 ,⑴若
,⑴若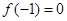 ,且函數(shù)
,且函數(shù) 的值域為
的值域為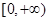 ,求
,求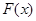 的表達式;
的表達式;
⑵設(shè) ,且函數(shù)
,且函數(shù) 為偶函數(shù),求證:
為偶函數(shù),求證: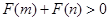 .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
用水清洗一堆蔬菜上殘留的農(nóng)藥,對用一定量的水清洗一次的效果作如下假定:用一個單位的水可洗掉蔬菜上殘留農(nóng)藥的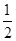 ,用水越多洗掉的農(nóng)藥量也越多,但總還有農(nóng)藥殘留在蔬菜上.設(shè)用
,用水越多洗掉的農(nóng)藥量也越多,但總還有農(nóng)藥殘留在蔬菜上.設(shè)用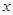 單位量的水清洗一次以后,蔬菜上殘留的農(nóng)藥量與本次清洗前殘留的農(nóng)藥量之比為函數(shù)
單位量的水清洗一次以后,蔬菜上殘留的農(nóng)藥量與本次清洗前殘留的農(nóng)藥量之比為函數(shù)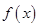 .
.
⑴試規(guī)定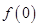 的值,并解釋其實際意義;
的值,并解釋其實際意義;
⑵試根據(jù)假定寫出函數(shù)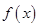 應(yīng)滿足的條件和具有的性質(zhì);
應(yīng)滿足的條件和具有的性質(zhì);
⑶設(shè)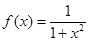 ,現(xiàn)有
,現(xiàn)有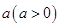 單位量的水,可以清洗一次,也可以把水平均分成兩份后清洗兩次.試問用那種方案清洗后蔬菜上殘留的農(nóng)藥量比較少?說明理由.
單位量的水,可以清洗一次,也可以把水平均分成兩份后清洗兩次.試問用那種方案清洗后蔬菜上殘留的農(nóng)藥量比較少?說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
甲、乙兩個工廠,甲廠位于一直線河岸的岸邊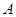 處,乙廠與甲廠在河的同側(cè),乙廠位于離河岸40千米的
處,乙廠與甲廠在河的同側(cè),乙廠位于離河岸40千米的 處,乙廠到河岸的垂足
處,乙廠到河岸的垂足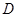 與
與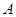 相距50千米,兩廠要在此岸邊
相距50千米,兩廠要在此岸邊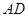 之間合建一個供水站
之間合建一個供水站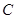 ,從供水站到甲廠和乙廠的水管費用分別為每千米3
,從供水站到甲廠和乙廠的水管費用分別為每千米3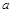 元和5
元和5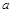 元,若
元,若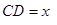 千米,設(shè)總的水管費用為
千米,設(shè)總的水管費用為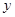 元,如圖所示,
元,如圖所示,
(1)寫出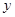 關(guān)于
關(guān)于 的函數(shù)表達式;
的函數(shù)表達式;
(2)問供水站 建在岸邊何處才能使水管費用最省?
建在岸邊何處才能使水管費用最省? 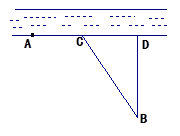
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
某漁業(yè)公司年初用49萬元購買一艘捕魚船,第一年各種費用6萬元,以后每年都增加2萬元,每年捕魚收益25萬元.
(1)問第幾年開始獲利?
(2)若干年后,有兩種處理方案:①年平均獲利最大時,以18萬元出售該漁船;②總純收入獲利最大時,以9萬元出售該漁船.問哪種方案最合算?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
設(shè)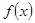 是定義在
是定義在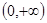 上的函數(shù),且
上的函數(shù),且 ,對任意
,對任意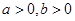 ,若經(jīng)過點
,若經(jīng)過點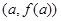 ,
,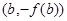 的直線與
的直線與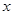 軸的交點為
軸的交點為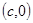 ,則稱
,則稱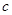 為
為 關(guān)于函數(shù)
關(guān)于函數(shù)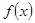 的平均數(shù),記為
的平均數(shù),記為 ,例如,當
,例如,當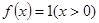 時,可得
時,可得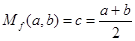 ,即
,即 為
為 的算術(shù)平均數(shù).
的算術(shù)平均數(shù).
當 時,
時, 為
為 的幾何平均數(shù);
的幾何平均數(shù);
當 時,
時, 為
為 的調(diào)和平均數(shù)
的調(diào)和平均數(shù) ;
;
(以上兩空各只需寫出一個符合要求的函數(shù)即可)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
(本題滿分14分)本題共有2個小題,第1小題滿分6分,第2個小題滿分8分。
某加油站擬造如圖所示的鐵皮儲油罐(不計厚度,長度單位:米),其中儲油罐的中間為圓柱形,左右兩端均為半球形,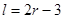 (
(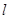 為圓柱的高,
為圓柱的高,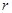 為球的半徑,
為球的半徑,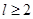 ).假設(shè)該儲油罐的建造費用僅與其表面積有關(guān).已知圓柱形部分每平方米建造費用為
).假設(shè)該儲油罐的建造費用僅與其表面積有關(guān).已知圓柱形部分每平方米建造費用為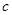 千元,半球形部分每平方米建造費用為3千元.設(shè)該儲油罐的建造費用為
千元,半球形部分每平方米建造費用為3千元.設(shè)該儲油罐的建造費用為 千元.
千元.
(1)寫出 關(guān)于
關(guān)于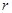 的函數(shù)表達式,并求該函數(shù)的定義域;
的函數(shù)表達式,并求該函數(shù)的定義域;
(2)求該儲油罐的建造費用最小時的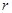 的值.
的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com