
甲、乙兩個(gè)工廠,甲廠位于一直線河岸的岸邊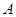 處,乙廠與甲廠在河的同側(cè),乙廠位于離河岸40千米的
處,乙廠與甲廠在河的同側(cè),乙廠位于離河岸40千米的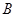 處,乙廠到河岸的垂足
處,乙廠到河岸的垂足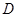 與
與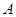 相距50千米,兩廠要在此岸邊
相距50千米,兩廠要在此岸邊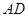 之間合建一個(gè)供水站
之間合建一個(gè)供水站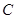 ,從供水站到甲廠和乙廠的水管費(fèi)用分別為每千米3
,從供水站到甲廠和乙廠的水管費(fèi)用分別為每千米3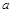 元和5
元和5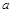 元,若
元,若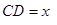 千米,設(shè)總的水管費(fèi)用為
千米,設(shè)總的水管費(fèi)用為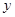 元,如圖所示,
元,如圖所示,
(1)寫出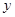 關(guān)于
關(guān)于 的函數(shù)表達(dá)式;
的函數(shù)表達(dá)式;
(2)問供水站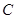 建在岸邊何處才能使水管費(fèi)用最省?
建在岸邊何處才能使水管費(fèi)用最省? 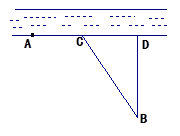
(1)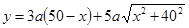 ,(2)A、D之間距甲廠20 km處
,(2)A、D之間距甲廠20 km處
解析試題分析:(1)由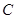 點(diǎn)的位置即可算出到甲、乙兩廠的距離,得出距離后總的水管費(fèi)用即可算出。(II)水管費(fèi)用最省,即求(1)式中
點(diǎn)的位置即可算出到甲、乙兩廠的距離,得出距離后總的水管費(fèi)用即可算出。(II)水管費(fèi)用最省,即求(1)式中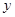 的最小值,利用求導(dǎo)數(shù)判斷函數(shù)的單調(diào)性即可得出結(jié)果。
的最小值,利用求導(dǎo)數(shù)判斷函數(shù)的單調(diào)性即可得出結(jié)果。
試題解析:(1)∵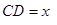 ,BD=40,AC=50-
,BD=40,AC=50- ,∴BC=
,∴BC=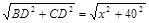
又總的水管費(fèi)用為y元,依題意有: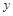 =3
=3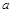 (50-x)+5
(50-x)+5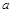
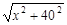
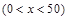 6分
6分
(2)由(1)得y′=-3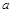 +
+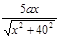 ,令y′=0,解得
,令y′=0,解得 =30 8分
=30 8分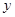 在(0,30)單調(diào)遞減,在(30,50)單調(diào)遞增上, 11分
在(0,30)單調(diào)遞減,在(30,50)單調(diào)遞增上, 11分
函數(shù)在 =30(km)處取得最小值,此時(shí)AC=50-
=30(km)處取得最小值,此時(shí)AC=50- ="20(km)" 13分
="20(km)" 13分
∴供水站建在A、D之間距甲廠20 km處,可使水管費(fèi)用最省. 14分
考點(diǎn):函數(shù)的應(yīng)用題及函數(shù)的單調(diào)性



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
經(jīng)英國相關(guān)機(jī)構(gòu)判斷,MH370在南印度洋海域消失.中國兩艦艇隨即在邊長為100海里的某正方形ABCD(如圖)海域內(nèi)展開搜索.兩艘搜救船在A處同時(shí)出發(fā),沿直線AP、AQ向前聯(lián)合搜索,且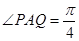 (其中點(diǎn)P、Q分別在邊BC、CD上),搜索區(qū)域?yàn)槠矫嫠倪呅蜛PCQ圍成的海平面.設(shè)
(其中點(diǎn)P、Q分別在邊BC、CD上),搜索區(qū)域?yàn)槠矫嫠倪呅蜛PCQ圍成的海平面.設(shè)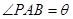 ,搜索區(qū)域的面積為
,搜索區(qū)域的面積為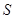 .
.
(1)試建立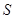 與
與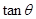 的關(guān)系式,并指出
的關(guān)系式,并指出 的取值范圍;
的取值范圍;
(2)求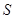 的最大值,并求此時(shí)
的最大值,并求此時(shí)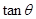 的值.
的值.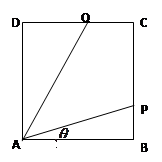
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖所示,n臺(tái)機(jī)器人M1,M2,……,Mn位于一條直線上,檢測臺(tái)M在線段M1 Mn上,n臺(tái)機(jī)器人需把各自生產(chǎn)的零件送交M處進(jìn)行檢測,送檢程序設(shè)定:當(dāng)Mi把零件送達(dá)M處時(shí),Mi+1即刻自動(dòng)出發(fā)送檢(i=1,2,……,n-1)已知Mi的送檢速度為V(V>0), 且 記
記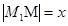 ,n臺(tái)機(jī)器人送檢時(shí)間總和為f(x).
,n臺(tái)機(jī)器人送檢時(shí)間總和為f(x).
 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
對于函數(shù) ,若存在實(shí)數(shù)對(
,若存在實(shí)數(shù)對( ),使得等式
),使得等式 對定義域中的每一個(gè)
對定義域中的每一個(gè)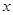 都成立,則稱函數(shù)
都成立,則稱函數(shù) 是“(
是“( )型函數(shù)”.
)型函數(shù)”.
(1) 判斷函數(shù)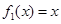 是否為 “(
是否為 “( )型函數(shù)”,并說明理由;
)型函數(shù)”,并說明理由;
(2) 若函數(shù)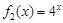 是“(
是“( )型函數(shù)”,求出滿足條件的一組實(shí)數(shù)對
)型函數(shù)”,求出滿足條件的一組實(shí)數(shù)對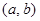 ;
;
(3)已知函數(shù) 是“
是“ 型函數(shù)”,對應(yīng)的實(shí)數(shù)對
型函數(shù)”,對應(yīng)的實(shí)數(shù)對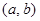 為
為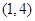 ,當(dāng)
,當(dāng)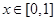 時(shí),
時(shí),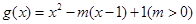 ,若當(dāng)
,若當(dāng)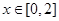 時(shí),都有
時(shí),都有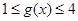 ,試求
,試求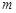 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知定義域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/6a/4/11v3z2.png" style="vertical-align:middle;" />的函數(shù) 同時(shí)滿足以下三個(gè)條件:
同時(shí)滿足以下三個(gè)條件:
①對任意的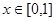 ,總有
,總有 ;
;
②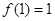 ;
;
③當(dāng)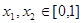 ,且
,且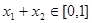 時(shí),
時(shí),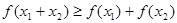 成立.
成立.
稱這樣的函數(shù)為“友誼函數(shù)”.
請解答下列各題:
(1)已知 為“友誼函數(shù)”,求
為“友誼函數(shù)”,求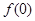 的值;
的值;
(2)函數(shù)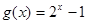 在區(qū)間
在區(qū)間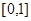 上是否為“友誼函數(shù)”?請給出理由;
上是否為“友誼函數(shù)”?請給出理由;
(3)已知 為“友誼函數(shù)”,假定存在
為“友誼函數(shù)”,假定存在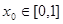 ,使得
,使得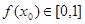 ,且
,且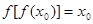 ,求證:
,求證: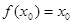 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)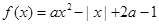 (
( 為實(shí)常數(shù)).
為實(shí)常數(shù)).
(1)若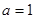 ,求函數(shù)
,求函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)設(shè) 在區(qū)間
在區(qū)間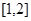 上的最小值為
上的最小值為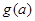 ,求
,求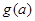 的表達(dá)式.
的表達(dá)式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(2014·孝感模擬)已知定義在區(qū)間[0,2]上的兩個(gè)函數(shù)f(x)和g(x),其中f(x)=-x2+2ax+1+a2,g(x)=x- +
+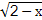 .
.
(1)求函數(shù)f(x)的最小值.
(2)對于?x1,x2∈[0,2],f(x1)>g(x2)恒成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
若函數(shù)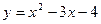 的定義域?yàn)閇0 ,m],值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/80/4/18s5t3.gif" style="vertical-align:middle;" />,則 m的取值范圍是______________
的定義域?yàn)閇0 ,m],值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/80/4/18s5t3.gif" style="vertical-align:middle;" />,則 m的取值范圍是______________
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com