
本題滿分12分)
一批救災物資隨26輛汽車從某市以x km/h的速度勻速開往相距400 km的災區.為安全起見,每兩輛汽車的前后間距不得小于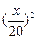 km,車速不能超過100km/h,設從第一輛汽車出發開始到最后一輛汽車到達為止這段時間為運輸時
km,車速不能超過100km/h,設從第一輛汽車出發開始到最后一輛汽車到達為止這段時間為運輸時 間,問運輸時間最少需要多少小時?
間,問運輸時間最少需要多少小時?
科目:高中數學 來源: 題型:解答題
(本題滿分10分)已知函數 ,(
,(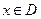 ),若同時滿足以下條件:
),若同時滿足以下條件:
① 在D上單調遞減或單調遞增
在D上單調遞減或單調遞增
② 存在區間[ ]
]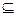 D,使
D,使 在[
在[ ]上的值域是[
]上的值域是[ ],那么稱
],那么稱 (
(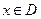 )為閉函數。
)為閉函數。
(1)求閉函數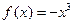 符合條件②的區間[
符合條件②的區間[ ];
];
(2)判斷函數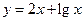 是不是閉函數?若是請找出區間[
是不是閉函數?若是請找出區間[ ];若不是請說明理由;
];若不是請說明理由;
(3)若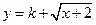 是閉函數,求實數
是閉函數,求實數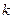 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
本題滿分12分,每小題各4分)
已知函數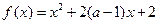 ,
,
(1)若函數 的值域為
的值域為 ,求實數a的值;
,求實數a的值;
(2)若函數 的遞增區間為
的遞增區間為 ,求實數a的值;
,求實數a的值;
(3)若函數 在區間
在區間
 上是增函數,求實數a的取值范圍.
上是增函數,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
.(12分)已知函數 的定義域為
的定義域為 ,且同時滿足:(Ⅰ)對任意
,且同時滿足:(Ⅰ)對任意 ,總有
,總有 ;(Ⅱ)
;(Ⅱ)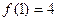 ;(Ⅲ)若
;(Ⅲ)若 ,則有
,則有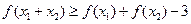
(1)試求 的值;
的值;
(2)試求函數 的最大值;
的最大值;
(3)試證明:當 時,
時, 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,某污水處理廠要在一個矩形污水處理池(ABCD)的池底水平鋪設污水凈化管道(Rt∆FHE,H是直角頂點)來處理污水,管道越長,污水凈化效果越好.設計要求管道的接口H是AB的中點,E,F分別落在線段BC,AD上.已知AB=20米,AD=10 米,記∠BHE=θ.
米,記∠BHE=θ.
(1)試將污水凈化管道的長度L表示為θ的函數,并寫出定義域;
(2)若sinθ+cosθ=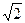 ,求此時管道的長度L;
,求此時管道的長度L;
(3)問:當θ取何值時,污水凈化效果最好?
并求出此時管道的長度.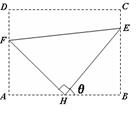
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)已知函數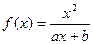 (a,b為常數)且方程f(x)-x+12=0
(a,b為常數)且方程f(x)-x+12=0
有兩個實根為x1="3," x2=4.(1)求函數f(x)的解析式;
(2)設k>1,解關于x的不等式;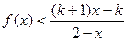 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
醫學上為了研究傳染病在傳播的過程中病毒細胞的生長規律及其預防措施,將 個病毒細胞注入到一只小白鼠的體內進行試驗.在試驗過程中,得到病毒細胞的數量與時間的關系記錄如下表:
個病毒細胞注入到一只小白鼠的體內進行試驗.在試驗過程中,得到病毒細胞的數量與時間的關系記錄如下表:
| 時間(小時) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 病毒細胞總數(個) |  | 2 | 4 | 8 | 16 | 32 | 64 |

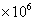 個時,小白鼠將死亡,但有一種藥物對殺死此種病毒有一定效果,用藥后,即可殺死其體內的大部分病毒細胞.
個時,小白鼠將死亡,但有一種藥物對殺死此種病毒有一定效果,用藥后,即可殺死其體內的大部分病毒細胞.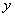 與時間
與時間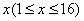 的函數關系式;
的函數關系式; )
)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某微機培訓機構打算購進一批微機桌和鼠標墊 ,市場價微機桌每張為150元,鼠標墊每個為5元,該培訓機構老板聯系了兩家商場甲和乙,由于用貨量大,這
,市場價微機桌每張為150元,鼠標墊每個為5元,該培訓機構老板聯系了兩家商場甲和乙,由于用貨量大,這 兩家商場都給出了優惠條件
兩家商場都給出了優惠條件
商場甲:買一贈一,買一張微機桌,贈一個鼠標墊
商場乙:打折,按總價的95%收款
該培訓機構需要微機桌 60張,鼠標墊
60張,鼠標墊 個(
個(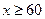 ),如果兩種商品只能在一家購買,請你幫助該培訓機構老板選擇在哪一家商場買更省錢?
),如果兩種商品只能在一家購買,請你幫助該培訓機構老板選擇在哪一家商場買更省錢?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com