
若函數 滿足:集合
滿足:集合 中至少存在三個不同的數構成等比數列,則稱函數
中至少存在三個不同的數構成等比數列,則稱函數 是等比源函數.
是等比源函數.
(Ⅰ)判斷下列函數:① ;②
;② ;③
;③ 中,哪些是等比源函數?(不需證明)
中,哪些是等比源函數?(不需證明)
(Ⅱ)判斷函數 是否為等比源函數,并證明你的結論;
是否為等比源函數,并證明你的結論;
(Ⅲ)證明: ,函數
,函數 都是等比源函數.
都是等比源函數.
(Ⅰ)①②③(Ⅱ)不是等比源函數(Ⅲ)略
解析試題分析:(Ⅰ)① 是等比源函數,例:當
是等比源函數,例:當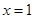 時,
時,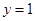 ;當
;當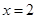 時,
時,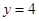 ;當
;當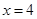 時,
時,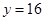 。1、4、16成等比。②
。1、4、16成等比。② 是等比源函數,例:當
是等比源函數,例:當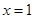 時,
時,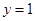 ;當
;當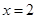 時,
時,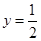 ;當
;當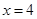 時,
時,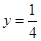 。
。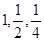 成等比。③
成等比。③ 是等比源函數,例:當
是等比源函數,例:當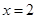 時,
時,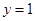 ;當
;當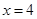 時,
時,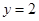 ;當
;當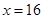 時,
時,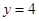 。1、2、4成等比數列。(Ⅱ)假設函數
。1、2、4成等比數列。(Ⅱ)假設函數 是等比源函數,即存在正整數
是等比源函數,即存在正整數 且
且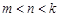 ,使得
,使得 成等比數列,根據等比中項列出式子,再推理論證得出矛盾。(Ⅲ)根據
成等比數列,根據等比中項列出式子,再推理論證得出矛盾。(Ⅲ)根據 可推導出
可推導出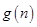 為首項為正整數公差也為正整數的等差數列。假設
為首項為正整數公差也為正整數的等差數列。假設 (
(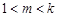 )整理得
)整理得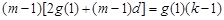 當
當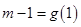 時說明假設成立,即函數
時說明假設成立,即函數 值中存在三個不同的數構成等比數列。
值中存在三個不同的數構成等比數列。
試題解析:(Ⅰ)①②③都是等比源函數. 3分
(Ⅱ)函數 不是等比源函數. 4分
不是等比源函數. 4分
證明如下:
假設存在正整數 且
且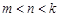 ,使得
,使得 成等比數列,
成等比數列,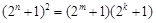 ,整理得
,整理得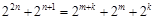 , 5分
, 5分
等式兩邊同除以 得
得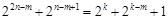 .
.
因為 ,所以等式左邊為偶數,等式右邊為奇數,
,所以等式左邊為偶數,等式右邊為奇數,
所以等式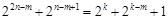 不可能成立,
不可能成立,
所以假設不成立,說明函數 不是等比源函數. 8分
不是等比源函數. 8分
(Ⅲ)法1:
因為 ,都有
,都有 ,
,
所以 ,數列
,數列 都是以
都是以 為首項公差為
為首項公差為 的等差數列.
的等差數列. ,
,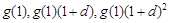 成等比數列,
成等比數列,
因為 ,
, ,
,
所以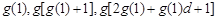
 ,
,
所以 ,函數
,函數 都是等比源函數. 13分
都是等比源函數. 13分
(Ⅲ)法2:
因為 ,都有
,都有 ,
,
所以 ,數列
,數列 都是以
都是以 為首項公差為
為首項公差為 的等差數列.
的等差數列.
由 ,(其中
,(其中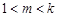 )可得
)可得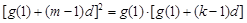 ,整理得
,整理得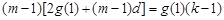 ,
,
令 ,則
,則 ,
,
所以

 ABC考王全優卷系列答案
ABC考王全優卷系列答案科目:高中數學 來源: 題型:解答題
已知A={x|ax-1>0},B={x|x2-3x+2>0}.
(1)若A∩B=A,求實數a的取值范圍;
(2)若A∩∁RB≠ ,求實數a的取值范圍.
,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設集合A為函數y=ln(-x2-2x+8)的定義域,集合B為函數y=x+ 的值域,集合C為不等式
的值域,集合C為不等式 (x+4)≤0的解集.
(x+4)≤0的解集.
(1)求A∩B;
(2)若C⊆∁RA,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com