
(本小題滿分13分)
已知函數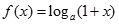 ,
,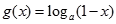 ,
,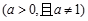 .
.
(Ⅰ)設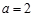 ,函數
,函數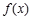 的定義域為
的定義域為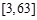 ,求函數
,求函數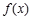 的最值;
的最值;
(Ⅱ)求使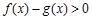 的
的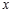 的取值范圍.
的取值范圍.
(I)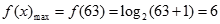 ,
,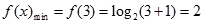
(II)①當 時,
時, 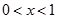 ;②當
;②當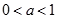 時,
時, 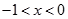 。
。
解析試題分析:(1)根據對數函數定義域,和單調性得到函數的最值(2)對于底數a,由于不定,需要分情況來討論得到。
解
(I)當 時,函數
時,函數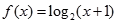 為
為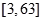 上的增函數........................3分
上的增函數........................3分
故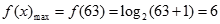 ,
,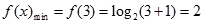 ..........................................6分
..........................................6分
(II) ,即
,即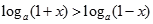 ,
,
①當 時,
時, ,得
,得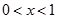 ........................................9分
........................................9分
②當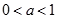 時,
時, ,得
,得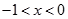 ..........................13分
..........................13分
考點:本試題主要考查了對數函數定義域的求解以及對數不等式的求解。
點評:解決該試題的關鍵是利用底數的大于1,還是底數大于零小于1,分情況來解決對數不等式的求解。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
(1)已知函數f(x)=2x-x2,問方程f(x)=0在區間[-1,0]內是否有解,為什么?
(2)若方程ax2-x-1=0在(0,1)內恰有一解,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)如下左圖,已知底角為450的等腰三角形ABC,底邊AB的長為2,當一條垂直于AB的直線L從左至右移動時,直線L把三角形ABC分成兩部分,令AD=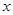 ,
,
(1) 試寫出左邊部分的面積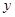 與x的函數解析式;
與x的函數解析式;
(2) 在給出的坐標系中畫出函數的大致圖象。 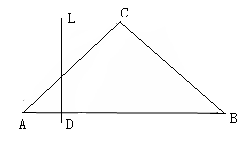
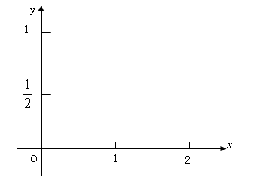
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com