
已知函數(shù)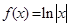
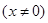 ,函數(shù)
,函數(shù)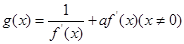
⑴當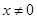 時,求函數(shù)
時,求函數(shù)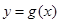 的表達式;
的表達式;
⑵若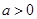 ,函數(shù)
,函數(shù)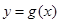 在
在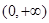 上的最小值是2 ,求
上的最小值是2 ,求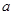 的值;
的值;
⑶在⑵的條件下,求直線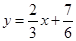
 與函數(shù)
與函數(shù)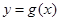 的圖象所圍成圖形的面積.
的圖象所圍成圖形的面積.
(1) 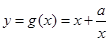 (2)
(2) 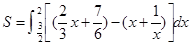 =
=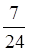 -
2ln2 +ln3
-
2ln2 +ln3
【解析】
導(dǎo)數(shù)部分的高考題型主要表現(xiàn)在:利用導(dǎo)數(shù)研究函數(shù)的性質(zhì),高考對這一知識點考查的要求是:理解極大值、極小值、最大值、最小值的概念,并會用導(dǎo)數(shù)求函數(shù)的單調(diào)區(qū)間、極大值、極小值及閉區(qū)間上的最大值和最小值。⑴∵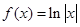 ,∴當
,∴當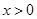 時,
時,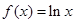 ;
當x<0時,
;
當x<0時,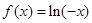 ∴當x>0時,
∴當x>0時,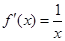 ;
………………2’
;
………………2’
當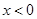 時,
時,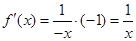
∴當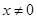 時,函數(shù)
時,函數(shù)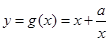 ………………………………………….4’
………………………………………….4’
⑵∵由⑴知當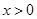 時,
時,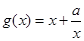 ,…………………………………………………..5’
,…………………………………………………..5’
∴當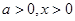 時,
時, 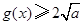 當且僅當
當且僅當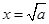 時取等號………………………7’
時取等號………………………7’
∴函數(shù)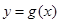 在
在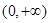 上的最小值是
上的最小值是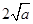 ,∴依題意得
,∴依題意得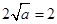 ∴
∴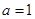 …….8’
…….8’
⑶由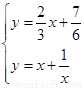 解得
解得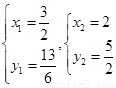 …………………………….10’
…………………………….10’
∴直線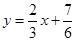 與函數(shù)
與函數(shù)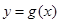 的圖象所圍成圖形的面積
的圖象所圍成圖形的面積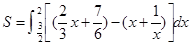 =
=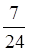 -
2ln2 +ln3
-
2ln2 +ln3


科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| e |
| 1 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| 2n |
 |
| i=1 |
| 2n |
 |
| i=1 |
| 1 | ||
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
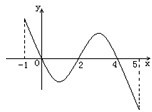 已知函數(shù)f(x)的定義域為[-1,5],部分對應(yīng)值如下表,f(x)的導(dǎo)函數(shù)y=f′(x)的圖象如圖所示.給出關(guān)于f(x)的下列命題:
已知函數(shù)f(x)的定義域為[-1,5],部分對應(yīng)值如下表,f(x)的導(dǎo)函數(shù)y=f′(x)的圖象如圖所示.給出關(guān)于f(x)的下列命題:| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| b |
| x |
| x |
| 2 |
| x |
| 2 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com