
如圖,在平面直角坐標系 中,以
中,以 軸為始邊,兩個銳角
軸為始邊,兩個銳角 ,
, 的終邊分別與單位圓相交于A,B 兩點.
的終邊分別與單位圓相交于A,B 兩點.
(Ⅰ)若 ,
, ,求
,求 的值;
的值;
(Ⅱ)若角 的終邊與單位圓交于
的終邊與單位圓交于 點,設角
點,設角 的正弦線分別為
的正弦線分別為 ,試問:以
,試問:以 作為三邊的長能否構成一個三角形?若能,請加以證明;若不能,請說明理由.
作為三邊的長能否構成一個三角形?若能,請加以證明;若不能,請說明理由.
(Ⅰ)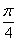 (Ⅱ)以
(Ⅱ)以 作為三邊的長能構成一個三角形.
作為三邊的長能構成一個三角形.
解析試題分析:(Ⅰ)∵0<α< , tanα=
, tanα=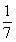 ,∴cosα=
,∴cosα= ,sinα=
,sinα= .
.
又∵0<β< ,sinβ=
,sinβ=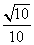 ,∴0<2β<π,cos2β=1-2sin2β=
,∴0<2β<π,cos2β=1-2sin2β=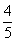 ,sin2β=
,sin2β=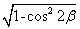 =
=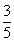 .
.
于是cos(α+2β)=cosαcos2β-sinαsin2β= ×
×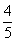 -
- ×
×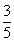 =
=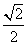 .
.
由已知條件知0<α+2β<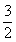 π,∴α+2β=
π,∴α+2β= . 6分
. 6分
(Ⅱ)解:以 作為三邊的長能構成一個三角形,證明如下:
作為三邊的長能構成一個三角形,證明如下:
∵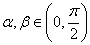 ,∴
,∴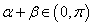
∴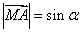 ,
,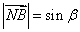 ,
,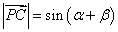
∵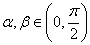 ,所以
,所以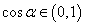 ,
,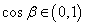 ,于是有:
,于是有: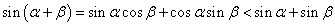 ① 8分
① 8分
又∵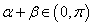 ,∴
,∴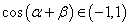 ,于是有:
,于是有: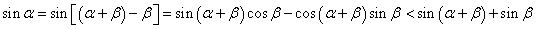 ②
②
同理: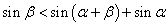 ③
③
由①②③可知,以 作為三邊的長能構成一個三角形. 12分
作為三邊的長能構成一個三角形. 12分
考點:同角間的三角函數關系及兩角和的余弦公式
點評:第一問涉及到基本公式有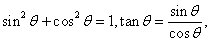
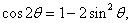
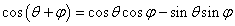 ,求角的大小常首先求角的某一三角函數值,結合角的范圍即可求出;第二問判定能否構成三角形即判定三邊長是否有任意兩邊之和大于第三邊,確定不等式關系主要借助于正余弦函數的有解性
,求角的大小常首先求角的某一三角函數值,結合角的范圍即可求出;第二問判定能否構成三角形即判定三邊長是否有任意兩邊之和大于第三邊,確定不等式關系主要借助于正余弦函數的有解性


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:解答題
閱讀下面材料:
根據兩角和與差的正弦公式,有 ------①
------① ------②
------②
由①+② 得 ------③
------③
令 有
有
代入③得  .
.
(Ⅰ)類比上述推證方法,根據兩角和與差的余弦公式,證明: ;
;
(Ⅱ)若 的三個內角
的三個內角 滿足
滿足 ,試判斷
,試判斷 的形狀.
的形狀.
(提示:如果需要,也可以直接利用閱讀材料及(Ⅰ)中的結論)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com