
閱讀下面材料:
根據兩角和與差的正弦公式,有 ------①
------① ------②
------②
由①+② 得 ------③
------③
令 有
有
代入③得  .
.
(Ⅰ)類比上述推證方法,根據兩角和與差的余弦公式,證明: ;
;
(Ⅱ)若 的三個內角
的三個內角 滿足
滿足 ,試判斷
,試判斷 的形狀.
的形狀.
(提示:如果需要,也可以直接利用閱讀材料及(Ⅰ)中的結論)
(1)結合兩角和的余弦公式來聯(lián)立方程組來求解得到。
(2)直角三角形
解析試題分析:解法一:(Ⅰ)因為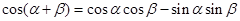 , ①
, ①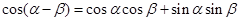 , ② 2分
, ② 2分
①-② 得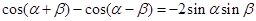 . ③ 3分
. ③ 3分
令 有
有 ,
,
代入③得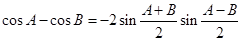 . 6分
. 6分
(Ⅱ)由二倍角公式, 可化為
可化為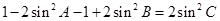 , 8分
, 8分
即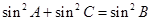 . 9分
. 9分
設 的三個內角A,B,C所對的邊分別為
的三個內角A,B,C所對的邊分別為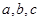 ,
,
由正弦定理可得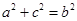 . 11分
. 11分
根據勾股定理的逆定理知 為直角三角形. 12分
為直角三角形. 12分
解法二:(Ⅰ)同解法一.
(Ⅱ)利用(Ⅰ)中的結論和二倍角公式,  可化為
可化為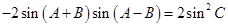 , 8分
, 8分
因為A,B,C為 的內角,所以
的內角,所以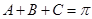 ,
,
所以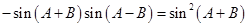 .
.
又因為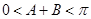 ,所以
,所以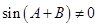 ,
,
所以 .
.
從而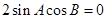 . 10分
. 10分
又因為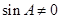 ,所以
,所以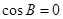 ,即
,即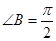 .
.
所以 為直角三角形. 12分
為直角三角形. 12分
考點:兩角和與差三角函數公式、二倍角公式
點評:本小題主要考查兩角和與差三角函數公式、二倍角公式、三角函數的恒等變換等基礎知識,考查推理論證能力,運算求解能力,考查化歸與轉化思想等


科目:高中數學 來源: 題型:解答題
如圖,在平面直角坐標系 中,以
中,以 軸為始邊,兩個銳角
軸為始邊,兩個銳角 ,
, 的終邊分別與單位圓相交于A,B 兩點.
的終邊分別與單位圓相交于A,B 兩點.
(Ⅰ)若 ,
, ,求
,求 的值;
的值;
(Ⅱ)若角 的終邊與單位圓交于
的終邊與單位圓交于 點,設角
點,設角 的正弦線分別為
的正弦線分別為 ,試問:以
,試問:以 作為三邊的長能否構成一個三角形?若能,請加以證明;若不能,請說明理由.
作為三邊的長能否構成一個三角形?若能,請加以證明;若不能,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com