
已知函數 為奇函數,且
為奇函數,且 在
在 處取得極大值2.
處取得極大值2.
(1)求函數 的解析式;
的解析式;
(2)記 ,求函數
,求函數 的單調區間。
的單調區間。
解:(1)由 (
( ≠0)為奇函數,
≠0)為奇函數,
∴ ,代入得,
,代入得, ………………………………………………1分
………………………………………………1分
∴ ,且
,且 在
在 取得極大值2.
取得極大值2.
∴ 解得
解得 ,
, ,∴
,∴ …………4分
…………4分
(2)∵ ,定義域為
,定義域為
∴ ……
…… …………………………………5分
…………………………………5分
1°當 ,即
,即 時,
時, ,函數在
,函數在 上單調遞減;………7分
上單調遞減;………7分
2°當 ,
, ,∵
,∵ ,∴
,∴
∴函數在 上單調遞減; ………………………………………………………9分
上單調遞減; ………………………………………………………9分
3°當 ,
, ,令
,令 ,∵
,∵ ,
,
∴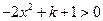 ,解得
,解得 ,結合
,結合 ,得
,得 ……11分[來源:Z。xx。k.Com]
……11分[來源:Z。xx。k.Com]
令 ,解得
,解得 ………………………………………12分
………………………………………12分
∴ 時,函數的單調遞增區間為
時,函數的單調遞增區間為 ,遞減區間為
,遞減區間為 ,………13分
,………13分
綜上,當 時,函數的單調遞減區間為
時,函數的單調遞減區間為 ,無單調遞增區間,
,無單調遞增區間,
當 時,函數的單調遞增區間為
時,函數的單調遞增區間為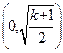 ,遞減區間為
,遞減區間為 …14分
…14分
解析


科目:高中數學 來源: 題型:解答題
已知函數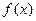 =
= ,
, .
.
(1)求函數 在區間
在區間 上的值域T;
上的值域T;
(2)是否存在實數 ,對任意給定的集合T中的元素t,在區間
,對任意給定的集合T中的元素t,在區間 上總存在兩個不同的
上總存在兩個不同的 ,使得
,使得 成立.若存在,求出
成立.若存在,求出 的取值范圍;若不存在,請說明理由;
的取值范圍;若不存在,請說明理由;
(3
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)
已知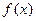 是定義在
是定義在 上的奇函數,當
上的奇函數,當 時
時
(1)求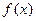 的解析式;
的解析式;
(2)是否存在實數 ,使得當
,使得當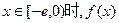 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com